Geometry & Recognition

FFT는 입력 데이터의 개수$(N)$가 2의 지수승으로 주어질 때  $O(N\log N)$의 연산만으로 빠르게 DFT을 수행하는 알고리즘이다. 주어진 $N$개의 data $\{F_0,F_1,...,F_{N-1}\}$의  DFT $\{a_0,a_1,...,a_{N-1}\}$는

$$a_k=\sum _{n=0}^{N-1}{F}_n\exp (-i\frac{2\pi nk}{N})=\sum _{n=0}^{N-1}{F}_n(W^n{)}^k,W=\exp (-i\frac{2\pi }{N})$$ 로 표현된다. $N$이 2의 지수승으로 주어지면 이 합은 $n$이 짝수인 항과 홀수인 항으로 아래처럼 분리할 수 있다:

$$\begin{array}{rl}{a}_k& =\sum _{n=0}^{N/2-1}{F}_{2n}(W^{2n}{)}^k+W^k\sum _{n=0}^{N/2-1}{F}_{2n+1}(W^{2n}{)}^k\\ & =\text{(N/2개 even 항에 대한 DFT)}+W^k\times \text{(N/2개 odd 항에 대한 DFT)}\\ & =e_k+W^k{o}_k\end{array}$$

더불어 주기성 때문에 $a_k$의 계산도 절반만 하면 된다: 

$$a_{k+N/2}=e_k-W^k{o}_k,k=0,1,...,N/2-1.$$

이는 원래의 문제가 처음 입력 데이터의 절반만 가지고 처리하는 두 개의 동일한 문제로 줄일 수 있음을 보여준다. 전형적인 divide and conquer 기법을 적용할 수 있는 구조이므로 매우 빠르게 연산을 수행할 수 있다(Cooley-Tukey algorithm). 역변환의 경우에는 twiddle factor $W$를 $W^{\ast }$로 바꾸면 되므로(전체 normalization factor $\frac{1}{N}$가 덧붙여진다) 코드에서 쉽게 수정할 수 있다: ${\mathtt{W}}_{\mathtt{i}\mathtt{m}}\to \mathtt{-}{\mathtt{W}}_{\mathtt{i}\mathtt{m}}$. 아래는 FFT를 재귀적으로 구현한 코드이다. 비재귀적 구현은 kipl.tistory.com/22, https://kipl.tistory.com/622에서 찾을 수 있다.

N=8일 때 전개:

$$\begin{array}{rl}& a_k\\ & =\sum _{n=0}^7{F}_n(W^n{)}^k\\ & =\sum _{n=0}^3{F}_{2n}(W^{2n}{)}^k+W^k\sum _{n=0}^3{F}_{2n+1}(W^{2n}{)}^k\\ & =[\sum _{n=0}^1{F}_{4n}(W^{4n}{)}^k+W^{2k}\sum _{n=0}^1{F}_{4n+2}(W^{4n}{)}^k]+W^k[\sum _{n=0}^1{F}_{4n+1}(W^{4n}{)}^k+W^{2k}\sum _{n=0}^1{F}_{4n+3}(W^{4n}{)}^k]\\ & =[(F_0+W^{4k}{F}_4)+W^{2k}(F_2+W^{4k}{F}_6)]+W^k[(F_1+W^{4k}{F}_5)+W^{2k}(F_3+W^{4k}{F}_7)]\\ & =[(F_{000}+W^{4k}{F}_{100})+W^{2k}(F_{010}+W^{4k}{F}_{110})]\\ & +W^k[(F_{001}+W^{4k}{F}_{101})+W^{2k}(F_{011}+W^{4k}{F}_{111})]\end{array}$$

$F_n$ 인덱스의 이진비트가 twiddle factor를 어떻게 곱해야 하는지 알려주고, 비트를 역으로 읽으면 계수가 나타나는 순서를 알 수 있게 한다.

#define TWOPI 6.28318530717958647693
void split(int N, double* data) {
    if (N == 8) {
        double t1 = data[4]; data[4] = data[1];
        double t2 = data[2]; data[2] = t1; data[1] = t2;
        t1 = data[5]; data[5] = data[3];
        t2 = data[6]; data[6] = t1; data[3] = t2; 
        return;
    }
    double *tmp = new double [N / 2];
    for (int i = 0; i < N / 2; i++)   //copy odd elements to tmp buffer;
        tmp[i] = data[2 * i + 1];
    for (int i = 0; i < N / 2; i++)   // move even elements to lower half;
        data[i] = data[2 * i];            
    for (int i = 0; i < N / 2; i++)   // move odd elements to upper half;
        data[i + N / 2] = tmp[i];     
    delete [] tmp;
}
void fft4(double *re, double *im) {
    double tr1 = re[0]-re[2]+im[1]-im[3];
    double ti1 = im[0]-im[2]-re[1]+re[3];
    double tr2 = re[0]+re[2]-re[1]-re[3];
    double ti2 = im[0]+im[2]-im[1]-im[3];
    double ti3 = im[0]-im[2]+re[1]-re[3];
    double tr3 = re[0]-re[2]-im[1]+im[3];
    re[0] = re[0]+re[2]+re[1]+re[3];
    im[0] = im[0]+im[2]+im[1]+im[3];
    re[1] = tr1; im[1] = ti1;
    re[2] = tr2; im[2] = ti2;
    re[3] = tr3; im[3] = ti3;
}
int fft ( int N, double* re, double* im ) {
    if (N <= 0 || N & (N-1)) return 0; // N is not a power of 2;
    if ( N < 2 ) return 1;
    else if (N == 2) {
        double tr1 = re[0]-re[1], ti1 = im[0]-im[1];
        re[0] = re[0]+re[1]; im[0] = im[0]+im[1]; 
        re[1] = tr1; im[1] = ti1; 
        return 1;
    }  else if (N == 4) {
        fft4(re, im);
        return 1;
    }
        
    split ( N, re);
    split ( N, im);
    fft ( N / 2, &re[    0], &im[    0] );
    fft ( N / 2, &re[N / 2], &im[N / 2] );
    for ( int k = 0; k < N / 2; k++ ) {
        double Ere = re[k];
        double Eim = im[k];
        double Ore  = re[k + N / 2];
        double Oim  = im[k + N / 2];
        double Wre =  cos ( TWOPI * k / N );  //real part of twiddle factor:W
        double Wim =  -sin ( TWOPI * k / N ); //imag part of twiddlw factor:W
        double WOre = Wre * Ore - Wim * Oim;
        double WOim = Wre * Oim + Wim * Ore;
        re[k] = Ere + WOre;
        im[k] = Eim + WOim;
        re[k + N / 2] = Ere - WOre;
        im[k + N / 2] = Eim - WOim;
    }
    return 1;
};

6개의 주파수 $\{f_i=2,5,9,11,21,29\text{Hz}\}$가 섞인 신호 $s(t)$를 $[0,1]$ 초 구간에서 일정한 간격으로 sampling 해서 64개 data를 얻고(Nyquist frequency = 32Hz), 이에 대해 FFT를 수행한다.

$$s(t)=\sum _{i=0}^5(i+1)\cos (2\pi f_{i}t)$$

int fft_test_main() {
    const int samples = 64;
    double re[samples], im[samples];
    const int nfreqs = 6;
    double freq[nfreqs] = {2, 5, 9, 11, 21, 29};
    for (int i = 0; i < samples; i++) {
        double signal = 0;
        for (int k = 0; k < nfreqs; k++) 
            signal += (k + 1) * cos(TWOPI * freq[k] * i / samples);
        re[i] = signal;
        im[i] = 0.;
    }
    fft(samples, &re[0], &im[0]);
    for (int i = 0; i < samples; i++) TRACE("%d, %f, %f\n", i, re[i], im[i]);
    return 0;
}

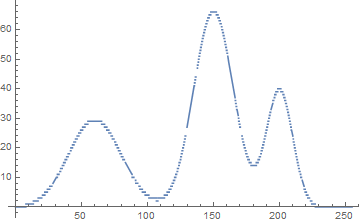
FFT 결과:

FFT2D

컬러를 양자화하는 방법으로 median-cut 알고리즘 이외에도 Octree을 이용한 알고리즘도 많이 쓰인다. (페인트샵 프로를 보면 이 두 가지 방법과 더불어 간단한 websafe 양자화 방법을 이용한다). Octree는 8개의 서브 노드를 가지는 데이터 구조이다. 이는 R, G, B의 비트 평면에서의 비트 값(각각의 레벨에서 8가지가 나옴)을 서브 노드에 할당하기 편리한 구조이다. 풀컬러를 이 Octree를 이용해서 표현을 하면 깊이가 9인 트리가 생성이 된다 (root + 각각의 비트 평면 레벨 = 8^8 = num of true colors). Octree  quantization은 이 트리의 깊이를 조절하여서 leaf의 수가 원하는 컬러 수가 되도록 조절하는 알고리즘이다. 전체 이미지를 스캔하면서 트리를 동적으로 구성하고 난 후 트리의 leaf의 수가 원하는 컬러수보다 작으면 각각의 leaf가 표현하는 컬러를 팔레트로 만들면 된다. 그러나 컬러를 삽입하면서 만들어지는 leaf의 수가 원하는 컬러 개수보다 많아지는 경우는 가장 깊은 leaf 노드를 부모 노드에 병합시켜서 leaf 노드의 수를 줄이는 과정을 시행한다. 이 병합 과정은 원래 leaf 노드들의 컬러 평균을 취하여 부모 노드에 전달한다. 따라서 Octree 알고리즘은 RGB 컬러에서 상위 비트가 컬러에 대표성을 가지도록 하위 비트 값을 병합하여서 컬러 수를 줄이는 방법을 이용한 것이다.
       
특정 RGB 비트 평면에서 R, G, B비트 값을 이용하여서 child-노드의 인덱스를 만드는 방법은

    child-node index = (R-비트<<2)|(G-비트<<1)|(B-비트) ;

     (R, G, B)=(109,204,170)의 경우;

      node |
      level | 0 1 2 3 4 5 6 7
     -------------------------
           R | 0 1 1 0 1 1 0 1
           G | 1 1 0 0 1 1 0 0
           B | 1 0 1 0 1 0 1 0
     ------|------------------
      child | 3 6 5 0 7 6 1 4
     index |
  
Octree 알고리즘은 컬러 이미지를 스캔하면서 트리를 동적으로 구성할 수 있으므로 median-cut 알고리즘보다도 메모리 사용에 더 효과적인 방법을 제공한다. 그리고 트리 깊이를 제한하여 일정 깊이 이상이 안되도록 만들 수 있으므로 빠른 알고리즘을 구현할 수 있다. 최종적으로  팔레트를 구성하는 컬러 값은 leaf 노드에 축적된 컬러의 평균값이 된다 (일반적으로 leaf-노드가 나타내는 비트 값과는 불일치가 생긴다). 이 알고리즘은 재귀적인 방법을 이용하면 쉽게 구현이 가능하고, 또한 웹상에서 구현된 소스도 찾을 수 있다.

참고 논문: "A Simple Method for Color Quantization: Octree Quantization." by M. Gervautz and W. Purgathofer 1988.

256 컬러 이미지(트리 깊이 = 5): RGB 값이 주어지면 전체 트리에서 해당 leaf을 찾아서 팔레트 인덱스를 얻는다. 이와는 다른 방법으로는 팔레트가 주어졌으므로 주어진  RGB 값과 가장 가까운 유클리디안 거리를 주는 팔레트의 인덱스를 할당하는 방법도 있다. 이 방법을 이용하면 아래의 결과와 약간 차이가 생긴다.

** 네이버 블로그에서 이전;

source code(C++): web.archive.org/web/20050306011057/www.drmay.net/octree/

Otsu 알고리즘은 이미지를 이진화시키는데 기준이 되는 값을 통계적인 방법을 이용해서 결정한다. 같은 클래스(전경/배경)에 속한 픽셀의 그레이 값은 유사한 값을 가져야 하므로 클래스 내에서 픽셀 값의 분산은 되도록이면 작게 나오도록 threshold 값이 결정되어야 한다. 또 잘 분리가 되었다는 것은 클래스 간의 거리가 되도록이면 멀리 떨어져 있다는 의미이므로 클래스 사이의 분산 값은 커야 함을 의미한다. 이 두 가지 요구조건은 동일한 결과를 줌을 수학적으로 보일 수 있다.

이미지의 이진화는 전경과 배경을 분리하는 작업이므로 클래스의 개수가 2개, 즉, threshold 값이 1개만 필요하다. 그러나 일반적으로 주어진 이미지의 픽셀 값을 임의의 개수의 클래스로 분리할 수도 있다. 아래의 코드는 주어진 이미지의 histogram을 Otsu의 아이디어를 이용해서 nclass개의 클래스로 분리하는 알고리즘을 재귀적으로 구현한 것이다. 영상에서 얻은 히스토그램을 사용하여 도수를 계산할 수 있는 0차 cumulative histogram($\mathtt{c}\mathtt{h}$)과 평균을 계산할 수 있는 1차 culmuative histogram($\mathtt{c}\mathtt{x}\mathtt{h}$)을 입력으로 사용한다. 

$$\mathtt{t}\mathtt{h}\mathtt{r}\mathtt{e}\mathtt{s}\mathtt{h}\mathtt{o}\mathtt{l}\mathtt{d}\mathtt{s}=\text{argmax}({\sigma }_B^2=\sum _{j=0}^{nclass-1}{\omega }_j{m}_j^2)$$

* Otsu 알고리즘을 이용한 이미지 이진화 코드: kipl.tistory.com/17

* 좋은 결과를 얻으려면 히스토그램에 적당한 필터를 적용해서 smooth하게 만드는 과정이 필요하다.

// 0 <= start < n;
double histo_partition(int nclass, double cxh[], int ch[], int n, int start, int th[]) {
    if (nclass < 1) return 0;
    if (nclass == 1) {
        int ws; double ms;
        if (start == 0) {
            ws = ch[n - 1];
            ms = cxh[n - 1] / ws;
        } else {
            ws = ch[n - 1] - ch[start - 1];             // start부터 끝까지 돗수;
            ms = (cxh[n - 1] - cxh[start - 1]) / ws;    // start부터 끝까지 평균값;
        }
        th[0] = n - 1;
        return ws * ms * ms;                            // weighted mean;
    }

    double gain_max = -1;
    int *tt = new int [nclass - 1];
    for (int j = start; j < n; j++) {
        int wj; double mj;
        if (start == 0) {
            wj = ch[j]; 
            mj = cxh[j];                    //mj = cxh[j] / wj;
        }
        else {
            wj = ch[j] - ch[start - 1];     //start부터 j까지 돗수;
            mj = (cxh[j] - cxh[start - 1]); //mj = (cxh[j] - cxh[start - 1]) / wj;
        }
        if (wj == 0) continue;
        mj /= wj;                           //start부터 j까지 평균;
        double gain = wj * mj * mj + histo_partition(nclass - 1, cxh, ch, n, j + 1, tt);
        if (gain > gain_max) {
            th[0] = j;
            for (int k = nclass - 1; k > 0; k--) th[k] = tt[k - 1];
            gain_max = gain;
        }
    }
    delete [] tt;
    return gain_max;
};

trimodal 분포의 분리;

class0: 0~th[0]

class1: (th[0]+1)~th[1],

class2: (th[1]+1)~th[2]=255

// recursive histo-partition 테스트;
// 0--t[0];--t[1];...;--t[nclass-2];t[nclass-1]=255=n-1;
// nclass일 때 threshold 값은 0---(nclss-2)까지;
double GetThreshValues(int hist[], int n, int nclass, int th[]) {
    if (nclass < 1) nclass = 1;
    // preparing for 0-th and 1-th cumulative histograms;
    int *ch = new int [n];          // cdf;
    double *cxh = new double [n];   //1-th cdf;
    ch[0] = hist[0];
    cxh[0] = 0; // = 0 * hist[0]
    for (int i = 1; i < n; i++) {
        ch[i] = ch[i - 1] + hist[i] ;
        cxh[i] = cxh[i - 1] + i * hist[i];
    }
    // nclass=1인 경우도 histo_partition()내에서 처리할 수 있게 만들었다.
    double var_b = histo_partition(nclass, cxh, ch, n, 0, th);
    delete [] ch;
    delete [] cxh;
    return var_b;
}