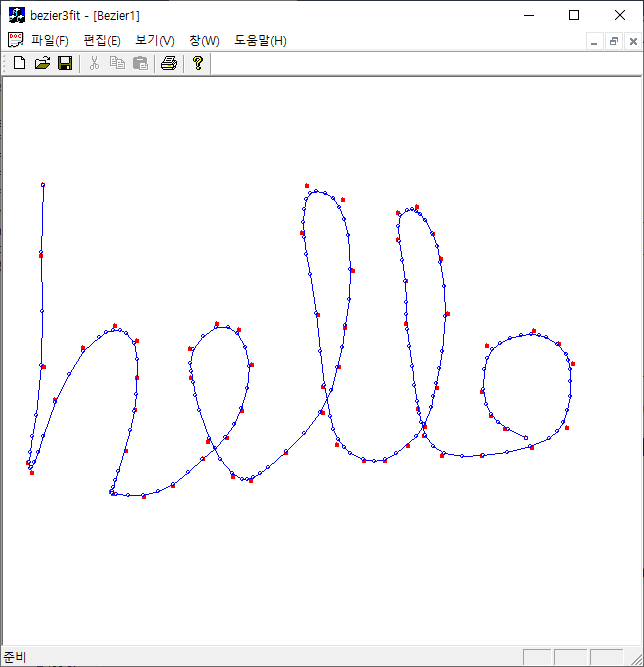
입력점들을 부드럽게 연결하는 베지어 곡선을 찾아보자. 입력점 사이 구간을 3차 베지어 곡선으로 표현하려면 4개의 컨트롤점이 필요한데, 최소자승법을 이용하지 않고 순차적인 3 입력점 $P_0, P_1, P_2$이 주어질 때 이를 이용해서 컨트롤 점을 구성한다.(따라서 베지어 곡선은 시작과 끝이 아닌 입력점을 일반적으로 통과하지 않는다) $$C_0 = (P_0+P_1)/2,~~C_1 = (P_0 +5 P_1)/6,~~C_2 = (5P_1+ P_2)/6,~~C_3=(P_1+P_2)/2$$ 컨트롤점으로 하는 베지어 곡선은 $[P_0, P_1, P_2]$의 일부분을 표현한다. 이 과정은 다음 한 입력점을 포함시켜서 다시 반복을 하는데 이 떄 이전 베이어 곡선의 마지막 컨트롤점($C_2$)이 새로이 만들어지는 베지어 곡선의 시작점($C_0^\text{new}$)이 되므로 두 베지어 곡선은 부드럽게 연결이 된다. 입력점의 시작과 끝점은 베이어 곡선이 통과하도록 컨트롤점에 포함되게 설계한다.
$$\text{front}:~ C_0=P_0, ~~C_1 = (P_0+2P_1)/3$$
$$\text{back}:~C_2=(2P_1+P_2)/3, ~~C_3=P_3$$
그리고 주어진 베지어 곡선의 분할은 균일한 간격으로 하지 않고, 각각의 구간에서 베지어 곡선이 충분히 평탄하도록 분할해서 저장한다.
// test flatness of a bezier curve with control points {p1, c1, c2, p2};
bool FlatBezier(const double eps,
const CfPt& p1, const CfPt& c1, const CfPt& c2, const CfPt& p2) {
CfPt U = c1 - (p1 * 2 + p2) / 3;
CfPt V = c2 - (p1 + p2 * 2) / 3;
double normU = hypot(U.x, U.y);
double normV = hypot(V.x, V.y);
return (3. * max(normU, normV) / 4.) <= eps;
}
// subdivision stage; De Casteljau's algorithm
void GetBezierPoints(const double eps,
const CfPt &p1, const CfPt &c1, const CfPt &c2, const CfPt &p2,
std::vector<CfPt>& smoothed) {
if (!FlatBezier(eps, p1, c1, c2, p2)) {
// Subdivide the curve at t = 0.5
// left;
CfPt mid_segm = (p1 + c1 * 3 + c2 * 3 + p2) / 8.0; // = B(1/2);
CfPt new_c1 = (p1 + c1) / 2.0;
CfPt new_c2 = (p1 + c1 * 2 + c2) / 4.0; // ((p1+c1)/2+(p1+c2)/2)/2
GetBezierPoints(eps, p1, new_c1, new_c2, mid_segm, smoothed);
// right;
new_c1 = (c1 + c2 * 2 + p2) / 4.0;
new_c2 = (c2 + p2) / 2.0;
GetBezierPoints(eps, mid_segm, new_c1, new_c2, p2, smoothed);
}
else smoothed.push_back(p2); // flat enough;
}
// linear interpolation between a and b;
// a와 b 사이를 (1-t): t로 내분;
CfPt lerp(const double t, const CfPt &a, const CfPt &b) {
return a * (1 - t) + b * t;
}
void SmoothPathWithBezier(std::vector<CfPt>& points, std::vector<CfPt>& smoothed) {
if (points.size() < 3) return ;
CfPt cntl[4];
CfPt *pts = &points[0]; // iterator;
const int N = points.size();
smoothed.clear();
smoothed.push_back(pts[0]);
for (int i = 2; i < N; i++, pts++) {
if (i == 2) {
cntl[0] = pts[0];
cntl[1] = lerp(2./ 3, pts[0], pts[1]);
} else {
//0번 control-pts= (0-1)의 중간점;
//1번 control-pts= (0-1)의 5:1 내분점;
cntl[0] = lerp(1./ 2, pts[0], pts[1]);
cntl[1] = lerp(5./ 6, pts[0], pts[1]);
}
if (i == N-1) {
//1:2 내분점;
cntl[2] = lerp(1./ 3, pts[1], pts[2]);
cntl[3] = pts[2];
} else {
//2번 control-pts;(1-2)의 1:5 내분점;
//3번 control-pts;(1-2)의 중간점;
cntl[2] = lerp(1./ 6, pts[1], pts[2]);
cntl[3] = lerp(1./ 2, pts[1], pts[2]);
}
//입력 중에 처음 두개가 같거나, 다음 두개가 같으면 마지막이 충분히 smooth하므로
// 마직막 control pt만 베지어 곡선에 삽입;
if ((pts[0] == pts[1]) || (pts[1] == pts[2]))
smoothed.push_back(cntl[3]);
else {
double tolerance = 1.; // 1-pixel;
GetBezierPoints(tolerance, cntl[0], cntl[1], cntl[2], cntl[3], smoothed);
}
}
}728x90
'Computational Geometry' 카테고리의 다른 글
| DDA Algorithm (0) | 2021.04.25 |
|---|---|
| B-Spline (0) | 2021.04.25 |
| Flatness of Cubic Bezier Curve (0) | 2021.04.23 |
| Convexity of Bezier Curve (0) | 2021.04.22 |
| De Casteljau's Algorithm (0) | 2021.04.22 |



