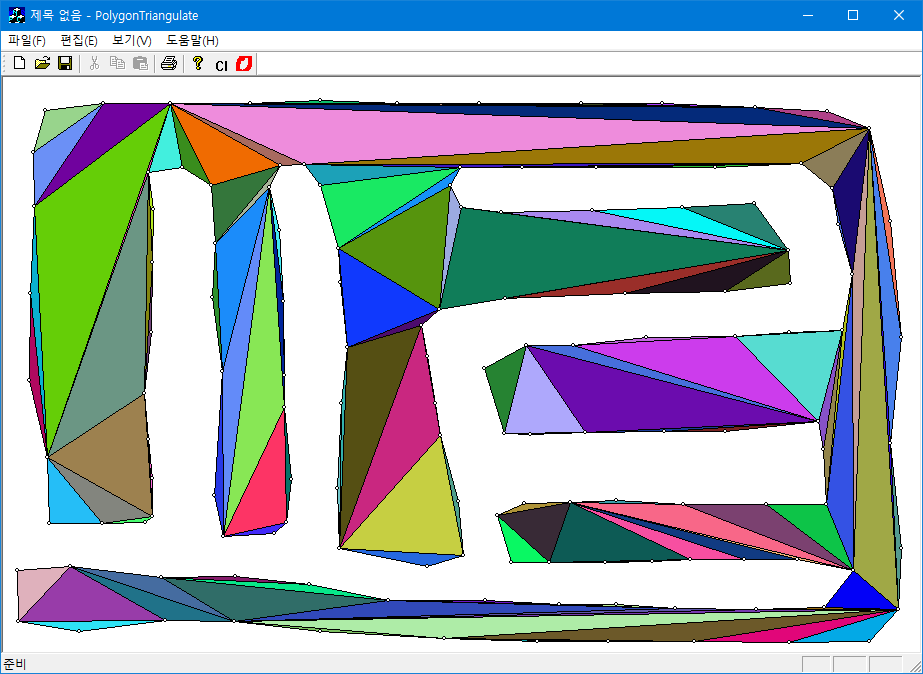
단순 다각형(simple polygon)의 삼각화 알고리즘의 다른 구현이다. 이전 구현과 같은 Ear-Clipping 알고리즘을 써서 구현한 것이다. 폴리곤의 각 꼭짓점을 돌면서 현재 꼭짓점의 직전과 직후의 꼭짓점들로 구성한 삼각형이 Ear인가를 체크해서 맞으면 이 삼각형을 추가하고, 현 꼭짓점은 주어진 폴리곤에서 제거를 한 후 나머지에 대해 테스트를 계속한다. $N$ 개의 꼭짓점을 가지는 단순 폴리곤의 경우에 $N-2$ 개의 삼각형으로 분해가 된다.
주어진 폴리곤이 시계방향으로 정렬된 경우는 반시계 방향으로 바꾸어서 정렬시킨 후 작업을 한다. 구현된 알고리즘의 복잡도는 ${\cal O}(N^2)$이다.
last update: 2012.10.03;
static bool leftSide(CPoint *P, CPoint *A, CPoint *B) {
// P가 선분(A,B)의 왼쪽 또는 위에 있는가?
return ((B->x - A->x) * (P->y - A->y) - ( B->y - A->y) * (P->x - A->x)) >=0;
}static bool insideTriangle (CPoint *P, CPoint *A, CPoint *B, CPoint *C) {
// 반시계방향으로 정렬된 삼각형(A,B,C)의 안에 점 P가 있는가?(경계포함);
if (!leftSide(P, A, B)) return false;
if (!leftSide(P, B, C)) return false;
if (!leftSide(P, C, A)) return false;
return true;
};static bool earTest(int a, int b, int c, int nv, int *V, CPoint *points) {
// Check the triangle {V[a], V[b], V[c]} is an Ear;
CPoint *A = &points[V[a]];
CPoint *B = &points[V[b]];
CPoint *C = &points[V[c]];
// colinear(A->B->C) or concave인가를 체크; 반시계 방향으로 정렬된 입력점이므로 왼편에
// 있으면 concave이므로 ear가 안된다;
if (leftSide(B, A, C)) return false;
// 이미 만들어진 삼각형의 꼭지점이 포함되는지 체크한다;
for (int k = 0; k < nv; ++k) {
if ((k == a) || (k == b) || (k == c)) continue;
if (insideTriangle(&points[V[k]], A, B, C)) return false;
}
return true;
};static double polygonArea2(std::vector<CPoint>& pts) {
double area2 = 0.;
for (int p = pts.size() - 1, q = 0; q < pts.size(); p = q++)
area2 += pts[p].x * pts[q].y - pts[p].y * pts[q].x;
return (area2);
}/* Polygon should be simple(ccw or cw);*/
bool polygonTriangulation(std::vector<CPoint>& pts, std::vector<Triangle>& triplets) {
if (pts.size() < 3) return 0;
triplets.clear(); triplets.reserve(pts.size() - 2);
std::vector<int> V(pts.size()); // contains vertex indices;
// 주어진 단순폴리곤을 반시계방향으로 정렬;
if (polygonArea2(pts) > 0)
for (int v = pts.size(); v-- > 0;) V[v] = v;
else
for (int v = pts.size(), k = 0; v-- > 0;) V[v] = k++;
// (pts.size()-2)개 꼭지점을 차례로 제거한다.
// 한개의 꼭지점이 제거될때마다 삼각형이 하나씩 생긴다;
int nv = pts.size();
int err_detect = 2 * nv; /* error detection */
for (int v = nv - 1; nv > 2; ) {
// 단순폴리곤이 아닌 경우에 무한루프를 도는 것을 방지;
if (0 >= (err_detect--)) {
TRACE("triangulate::ERROR\n");
return false;
}
// <u,v,w>는 연속하는 세 꼭지점의 인덱스임;
int u = v % nv;
v = (u + 1) % nv;
int w = (v + 1) % nv;
if (earTest(u, v, w, nv, &V[0], &pts[0])) {
triplets.push_back(Triangle(pts[V[u]], pts[V[v]], pts[V[w]]));
// 꼭지점 V[v]를 제거함;
for (int k = v, j = k + 1; j < nv;) V[k++] = V[j++];
--nv;
/* resest error detection counter */
err_detect = 2 * nv;
}
}
return triplets.size() == (pts.size() - 2); // # of triangle = (# of pts-2);
};
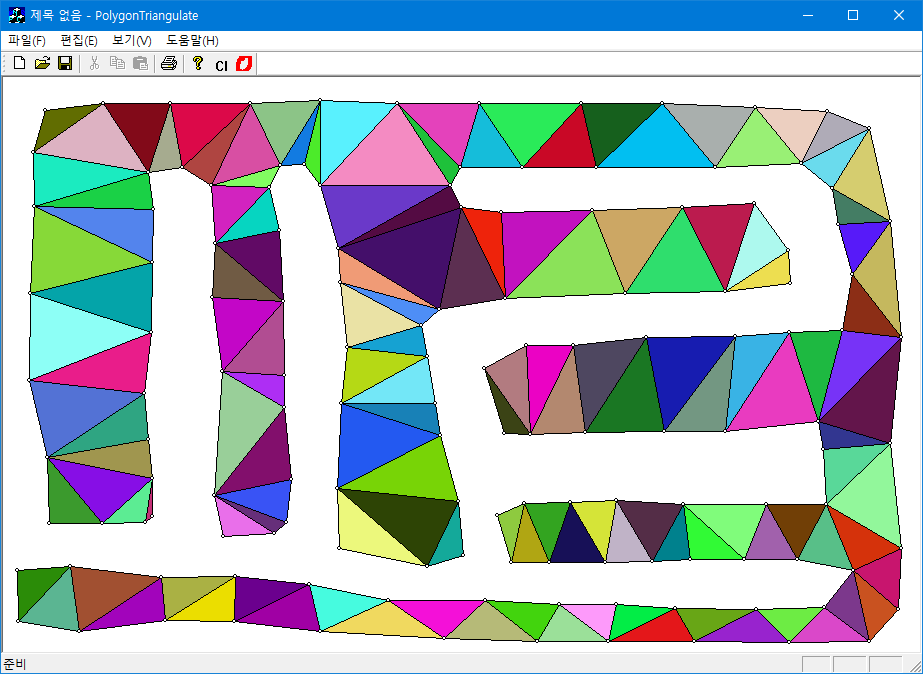
최적화 후:
'Computational Geometry' 카테고리의 다른 글
| Wu's Line Algorithm (1) | 2008.06.02 |
|---|---|
| Brute Force Triangulation (1) | 2008.05.28 |
| Polygon Triangulation (4) | 2008.05.25 |
| Polygon Fill (0) | 2008.05.22 |
| Fortune's Sweep Algorithm (0) | 2008.05.22 |




