Processing math: 100%

Fast Float Sqrt

Image Recognition/Fundamental 2020. 12. 27. 12:14

이미지 처리 연산 과정에서 제곱근 값을 계산해야 경우가 많이 생긴다. 이 경우 math-라이브러리의 sqrt() 함수를 사용하는 것보다 원하는 정밀도까지만 계산을 하는 근사적인 제곱근 함수를 만들어서 사용하는 것이 계산 비용 측면에서 유리할 수 있다. 

주어진 양수 x의 제곱근 y=√x를 구하는 것은 F(y)=y2−x의 근을 구하는 것과 같다. 프로그램적으로 근은 반복적인 방법에 의해서 구해지는데 많이 사용하는 알고리즘 중 하나가 Newton 방법이다. Newton 방법은 한 단계에서 근의 후보가 정해지면 그 값에서 F에 접하는 직선을 구한 후 그 직선이 가로축과 만나는 점을 다시 새로운 근으로 잡는 반복 과정을 일정한 에러 범위 내에 들어올 때까지 수행한다.

 

함수 F(y)의 근은 아래의 점화식에 의해서 구해지게 된다:

y(n+1)=y(n)−F(y(n))/F′(y(n)),n=0,1,2,...;

제곱근의 경우에는 (F(y)=y2−x) 점화식은 

y(n+1)=(y(n)+x/y(n))/2;

의 형태로 주어진다. 그러나, 이 점화식에는 계산 부하가 상대적으로 큰 나누기 연산이 들어 있다. 그런데 √x=x×(1/√x)로 표현할 수 있으므로 제곱근의 역수를 쉽게 계산하는 알고리즘을 찾으면 된다. x의 제곱근의 역수를 구하는 점화식은 (이 경우 F(y)=1/y2−x)

y(n+1)=y(n)∗(3−y(n)∗y(n)∗x)/2;

이므로 전체적인 제곱근을 구하는 pseudo 코드는

float fast_sqrt(float x) {
    xhalf = 0.5F * x;
    y = initial_guess_of (1/sqrt(x));
    while (error is not small)
        // find approx inverse sqrt root of (x);
        y = y * 1.5 - y * y * y * xhalf;
    end while

    // finally return sqrt(x) = x * (1 / sqrt(x));
    return (x * y);
}

보통 iteration 횟수는 고정이 되어 있다. 남은 문제는 초기값 추정뿐이다. Newton 방법에서 잘 추정된 초기값은 몇 번의 반복으로도 원하는 정밀도를 얻을 수 있게 하지만 잘못된 추정은 수렴 속도를 더디게 한다. 또한 초기값의 추정 과정도 매우 간단해야 하는데, 좋은 추정을 하기 위해서는 IEEE에서 규정하는 double/float 포맷에 대한 정보와 수치해석 지식이 필요하다.

 

IEEE의 32비트 float 상수의 비트 구성은 0∼22번째 비트까지는 소수점 아래의 유효숫자(Mantissa: M)를 표기하고, 23번째부터 30번째까지는 지수 부분(Exponent: E)을 표시하는데 127만큼 더해진 값이다(+-지수를 표현하기 위한 것으로 실제 지수는 e=E−127). 마지막 31비트는 부호를 결정한다.

임의의 양의 float 상수 x>0가 

x=(−1)0×2(b30b29....b23)2−127×(1.b22b21...b0)2=2E−127(1+23∑i=1b23−i2−i)=(1+M)2E−127=(1+M)2e;

로 쓰여지면, 정수로 변환된 비트 데이터는 ix=∗(int ∗)&x=(E+M)223의 값을 갖는다. x 제곱근의 역수는

1√x=1√1+M2−e/2;

로 표현되므로 비트 데이터에서 지수부는 (−e/2)+127=190−E/2로 표현된다. 

 

이제 필요한 것은 잘 선택된 1/√x의 초기값을 찾는 것으로, 첫 번째로 시도할 근사는 유효숫자 부분 (1/√1+M)을 제거하고, 단순히 지수 부분(2−e/2)만 살리면 된다. 정수 표현으로 바꾸면 190이 23에서 30번째 비트를 채우도록 23을 시프트 하고, −E/2 부분은 원래 float 상수의 정수 표현을 나누면 유효숫자 부분에 해당하는 정도만 에러가 발생한다:

   정수 표현 = (190 - E / 2) << 23;

                  = (190 << 23) - (x의 정수형 변환 & (0xFF << 23)) >> 1;

                  ~ (190 << 23) - (x의 정수형 변환) >> 1;    // 유효 숫자 / 2 만큼 에러 발생;

                  = 0x5F000000 - (*(int *)&x) >> 1;

유효숫자 부분은 좀 더 높은 초기 정밀도를 갖도록 근사를 할 수 있는데 결과만 쓰면 0x5F000000 대신에 0x5F3759DF를 이용하면 된다.

//빠른 float 제곱근의 역수;
float fast_invsqrt(float x) {
    float xhalf = 0.5F * x;
    // initial guess of 1 / sqrt(x);
    int i = 0x5F3759DF - (*(int *)&x) >> 1;
    x = *(float *)&i;    
    //iterate
    x = x * (1.5F - x * x * xhalf);
    x = x * (1.5F - x * x * xhalf);
    // end of calculation of 1 / sqrt(x);
    return (x);
};
// 빠른 float 제곱근;
float fast_sqrt(float x) {
    float xhalf = 0.5F * x;
    //initial guess of 1 / sqrt(x);
    int i = 0x5F3759DF - (*(int *)&x) >> 1;
    float y = *(float *)&i;    
    //iterate
    y = y * (1.5F - y * y * xhalf);
    y = y * (1.5F - y * y * xhalf);
    //end of calculation of 1/sqrt(x);
    //return sqrt(x)=x * 1/sqrt(x);
    return (x * y)   
};

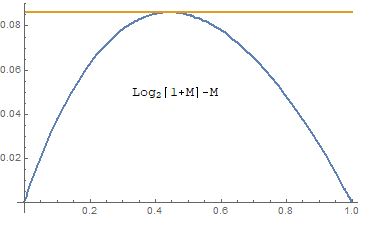
log2(x)=e+log2(1+M)이므로 x의 근삿값은 log2(1+M)의 근삿값을 잘 선택하면 된다. 함수 f(M)=log2(1+M)−M는 M=1/ln(2)−1에서 최댓값 0.0860713을 가지므로

0≤log2(1+M)−M≤0.0860713

이다. 따라서 오차를 최댓값의 절반으로 잡아서 근사하면

log2(1+M)≈M+δ,δ=0.08607132=0.0430385 

그리고 δ는 x에 무관한 값이 된다. x의 비트 데이터를 정수로 표현하면

ix=223(E+M)=223(e+δ+M)+223(127−δ)≈223log2(x)+223(127−δ). 로 근사할 수 있다. 두 번째 항은 x에 무관한 값이다. 따라서, 제곱근의 역수에 해당하는 비트 데이터의 근사적인 정수 표현은

i1√x≈223log2(1/√x)+223(127−δ)≈32223(127−δ)−12ix

로 쓸 수 있고, 위에서 구한 δ을 대입하면

i1√x≈0x5F37BCB6−ix>>1 

을 얻을 수 있다. δ=0.0450466을 대입하면 위에 적힌 코드에서 사용한 0x5F3759DF가 됨을 알 수 있다. 그러나 어떤 근거로 이 값을 선택했는지는...

728x90
저작자표시 비영리 변경금지

'Image Recognition > Fundamental' 카테고리의 다른 글

Edge and Corner Detection  (0) 2021.01.27
점증적인 cosine/sine 값 계산  (1) 2020.12.28
2차원 Gaussian 분포 생성(Creating a 2d Gaussian Distribution)  (0) 2020.12.10
PCA Line Fitting  (0) 2020.11.12
Histogram Equalization  (0) 2020.11.12
,

티스토리툴바