L=1 H, C=1 F일 때 impedence의 recursion relation은

Zn(s)=s+1sZn−1(s)1s+Zn−1(s)이므로 n→∞일 때 Z(s)=s+Z(s)1+sZ(s)
이어서 임피던스는 Z(s)=s+√4+s22로 구해진다. 따라서 전류는
I(s)=E(s)Z(s)=2E(s)s+√4+s2이므로 inverse Laplace 변환을 취하면 I(t)=L−1[I](t)=12πi∫γ+i∞γ−i∞2E(s)s+√4+s2estds
만약 t=0일 때 단위 스텝전압(E(t)=θ(t))을 가하는 경우 E(s)=1/s이고 전류는
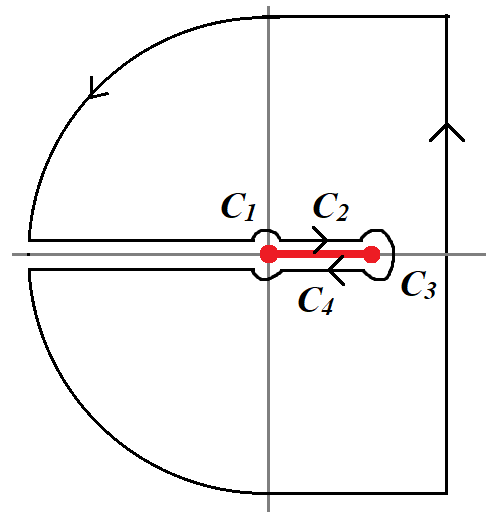
I(t)=12πi∫γ+i∞γ−i∞2s+√4+s2estdss이다. 이 Bromwich 적분을 그림과 같은 경로에 대한 적분으로 변환하면(https://kipl.tistory.com/653 참고)
I(t)=12πi(∫C1+∫C2+∫C3+∫C4+∫Cϵ)2z+√4+z2eztdzz 그러면 각 경로에서,
C1: z=yeiπ/2, z−2i=(2−y)ei3π/2, z+2i=(2+y)eiπ/2, y:2→0
C2: z=yeiπ/2, z−2i=(2+y)e−iπ/2, z+2i=(2−y)eiπ/2, y:0→2
C3: z=ye−iπ/2, z−2i=(2+y)e−iπ/2, z+2i=(2−y)eiπ/2, y:0→2
C4: z=ye−iπ/2, z−2i=(2−y)ei3π/2, z+2i=(2+y)eiπ/2, y:2→0
따라서
∫C1=∫022iy−√4−y2eiytdyy
∫C2=∫202iy+√4−y2eiytdyy
∫C3=∫022−iy+√4−y2e−iytdyy
∫C4=∫202−iy−√4−y2e−iytdyy
그리고 simple pole z=0을 감싸는 적분은 (z=ϵeiθ)
∫Cϵ=2πi
이므로 f(t)는 다음과 같이 쓸 수 있다.

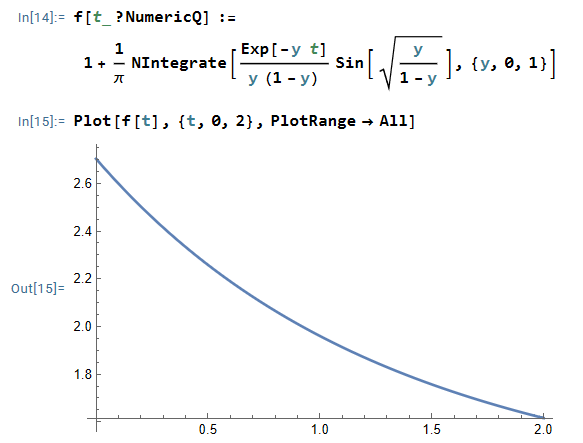
I(t)=1+1π∫20√4−y2sin(yt)dyy


I(t)=1+1π∫20√4−y2sin(yt)dyy
'Mathematics' 카테고리의 다른 글
| Integration along a branch cut-029 (0) | 2024.10.28 |
|---|---|
| Fourier transform inversion using a contour integral (0) | 2024.10.26 |
| Inverse Laplace Transform을 이용한 열방정식 해 (1) | 2024.10.23 |
| Inverse Laplace Transform as Bromwich Integral-4 (0) | 2024.10.22 |
| Inverse Laplace Transform as Bromwich Integral-3 (0) | 2024.10.20 |