Geometry & Recognition

$$I = \int_{0}^{3} \frac{  \sqrt[3]{ x (3-x)^2 }dx }{1+x} = \frac{\pi}{\sqrt{3}} \left( 6-  4\times 2 ^{1/3} \right) \approx 0.554439 \times \pi$$

복소함수

$$f(z) = \frac{\sqrt[3]{ z (3-z)^2}}{1+z}$$ 의 적분을 고려하자. Branch point가 $z=0,1$이므로 cutline을 $0 \le x  \le 3$으로 선택하자. 그러면 위상은 

$$0 \le \arg(z),~\arg(z-3) \le 2\pi$$

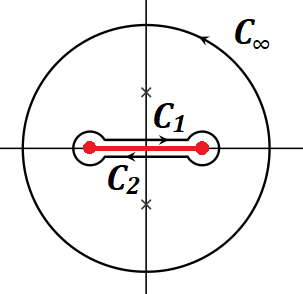
로 선택할 수 있다. 적분경로는 cutline을 감싸는 dog bone 모양과 반지름 $R > 3$인 원 $C_R$로 잡는다.

$z=-1$은 $f(z)$의 simple pole이고 residue는 

$$\text{Res} f(-1) = \left( e^{i\pi} (4 e^{i\pi})^2 \right)^{1/3} = - 4^{2/3}$$

이다. 또, 무한대에서 residue를 갖으므로 $C_R$에서 적분은

$$f(z) = \frac{(1-3/z)^{2/3}}{1+1/z} = 1- \frac{3}{z}+\cdots \quad \\ \to~~  \int_{C_R} f(z)dz =-2\pi i \times \text{Res}f(\infty) = -6\pi i$$ 로 계산된다.

$C_1$에서 $z= x e^{i0}$, $z-3= (3-x)  e^{i\pi }, ~(x:-1\to 1)$이므로 

$$\int_{C_1} f(z)dz = \int_{-1}^{1} \frac{ \sqrt[3]{x(3-x)^2 }   e^{i 2\pi/ 3}dx} {1+x} =  e^{i 2\pi/3} I$$

$C_2$에서 $z= x e^{i 2\pi}$, $z-3=(3-x) e^{i\pi}, ~(x:1\to-1)$이므로

$$\int_{C_2} f(z) dz = \int_{1}^{-1} \frac{ \sqrt[3]{x(3-x)^2} e^{i 4\pi/3} dx}{1+x}= - e^{i 4\pi/3} I$$

따라서 residue 정리에 의해서

$$\int_{C_1+C_2+C_\epsilon+C'_\epsilon} f(z)dz + \int_{C_R} f(z) dz = 2\pi i \times \text{Res}f(-1) \\ \to~~( e^{i 2\pi/3} - e^{i 4\pi/3}) I - 6\pi i  = 2\pi i \left(- 4^{2/3} \right) \\ I = \frac{\pi}{\sqrt{3}} \left( 6 - 4\times 2^{1/3} \right)$$

$$I = \int_{0}^{1} \frac{x\sqrt{x}  dx}{(1+x^2)\sqrt{1-x}} = \pi \left(1-\frac{1}{2}\sqrt{1+\sqrt{2}} \right) \approx  \pi \times  0.223113$$

복소함수 

$$f(z)  = \frac{z\sqrt{z}}{(1+z^2)\sqrt{1-z}}$$ 의 적분을 고려한다.

제곱근 함수 때문에 branch cut을 도입을 해야 하는데, branch point가 $z=0,1$이므로 이 두 점을 잇는 선분을 cut line으로 선택하자. 그러면 다음과 같이 위상을 선택할 수 있다.

$$-\pi \le \arg(z) \le \pi, \quad 0\le \arg (1-z) \le 2\pi$$ 적분경로는 cut line을 시계방향으로 감싸는 dog bone 모양과 $C_\infty$로 잡는다.

그러면 $z=\pm$가 $f(z)$의 simple pole이고 residue는 각각

$$\text{Res}f(z=i) = \frac{i e^{i\pi/4}}{2i \sqrt{2} e^{i7\pi/8}}= \frac{e^{-i5\pi/8}}{2\sqrt{2}} \\ \text{Res}f(z=-i) = \frac{-i e^{-i\pi/4}}{-2i \sqrt{2} e^{i\pi/8}}=\frac{e^{-i3\pi/8}}{2\sqrt{2}}$$

$C_1$에서 $z= xe^{i0}$, $z-1= (1-x) e^{i\pi} \to  1-z=(1-x)e^{i2\pi}, ~(x:-1\to 1)$이므로 

$$\int_{C_1} f(z) dz = \int_{-1}^{1} \frac{x\sqrt{x} dx}{(1+x^2) \sqrt{1-x} e^{ i\pi}}= -I$$

$C_2$에서 $z= xe^{i0}$, $z-1=(1-x) e^{i\pi} \to 1-z= (1-x) e^{i0},~(x:1\to -1)$이므로

$$\int_{C_2} f(z)dz = \int_{1}^{-1} \frac{x\sqrt{x}dx}{(1+x^2)\sqrt{1-x}} = -  I$$

그리고 $C_\infty$에서는 $z = R e^{i \theta }$이므로

$$\int _{C_\infty} f(z)dz= \int_0 ^{2\pi}  \frac{R\sqrt{R} (i Re^{i \theta}d \theta)}{R^2( i\sqrt{ R})} = 2\pi$$  

따라서 residue 정리에 의해서

$$\int_{C_1+C_2+C_\epsilon +C'_\epsilon+ C_\infty} f(z)dz = -I -I +2\pi   = 2\pi i \left( \text{Res}f(i) + \text{Res}f(-i)\right)\\ = \pi \sqrt{1+\sqrt{2}} \\ \quad \to \quad I = \pi \left(1 -\frac{1}{2}\sqrt{1+\sqrt{2}} \right)$$  

$$I = \int_{-1}^{1} \frac{ dx}{(1+x^2) \sqrt{1-x^2} } = \frac{ \pi}{\sqrt{2}}$$

복소함수

$$f(z) = \frac{1}{(1+z^2) \sqrt{1-z^2}}$$ 의 contour integral을 고려하자.

제곱근 함수때문에 branch cut을 잡아야 하는데, $-1 \le x \le 1$로 선택하자. 그러면 위상은 $0 \le \text{arg}(1-z) \le 2\pi$, $-\pi \le  \text{arg}(z+1) \le \pi$로 설정될 수 있다.

그리고 $z=\pm i$는 $f(z)$의 simple로 residue는 $z=i$일 때 

$$z-1=\sqrt{2} e^{ i 3\pi/4} \to 1-z= \sqrt{2} e^{i 7\pi / 4}, ~z+1 = \sqrt{2} e^{i \pi / 4}\\ \to~~ \sqrt{1-z^2}= \sqrt{2}  e^{i\pi} = -\sqrt{2} \\ \to \text{Res}f(z=i) = \frac{1}{-2i\sqrt{2}}$$ 그리고 $z=-i$에서는 $$z-1= \sqrt{2} e^{i 5\pi/4} \to 1-z= \sqrt{2} e^{i \pi / 4}, ~z+1 = \sqrt{2} e^{-i\pi / 4} \\ \to~~ \sqrt{1-z^2}= \sqrt{2}  e^{i 0} =  \sqrt{2} \\ \to \text{Res}f(z=-i) = \frac{1}{-2i \sqrt{2}}$$

$C_1$ 경로에서 $z-1=(1-x)e^{i\pi} \to 1-z = (1-x) e^{i 2\pi}$, $z+1 = (1+x) e^{i 0}~(x:-1 \to 1)$이므로 

$$\int_{C_1} f(z) dz = \int_{-1}^1 dx \frac{dx}{(1+x^2) \sqrt{1-x^2} e^{ i\pi } } =  -  I$$

$C_2$ 경로에서 $z-1=(1-x) e^{i\pi} \to 1-z = (1-x) e^{i 0}$, $z+1 = (1+x) e^{i 0} ~(x: 1 \to -1)$이어서

$$\int_{C_2} f(z) dz = \int_{1}^{-1} dx \frac{dx}{(1+x^2) \sqrt{1-x^2}  e^{ i 0} } = - I$$

그리고 $C_\epsilon$, $C'_\epsilon$, $C_\infty$에서 적분값은 0에 수렴하므로 residue 정리에 의해서 

$$-2I = 2 \pi i \times \left( \frac{1}{-2i\sqrt{2}}  + \frac{1}{-2i\sqrt{2}}\right)\qquad \to \qquad I  = \frac{\pi}{\sqrt{2}}$$