타원은 베지어 곡선을 이용해서 근사적으로 표현할 수 있음을 잘 알고 있다(https://kipl.tistory.com/313). 표준형 타원의 경우 1사분면에서 표현만 알면 대칭성에 의해서 나머지 사분면에서는 바로 구할 수 있으므로 거리를 구하는 점이 1사분면에 있는 경우만 알아보면 충분하다. 장축 반지름이 $a$, 단축 반지름이 $b$인 타원은 다음과 같이 베이지 곡선으로 표현된다.
Bezier Curve Approximation of an Ellipse
Bezier 곡선을 이용한 원의 근사처럼 타원을 근사해보도록 하자. 원점을 중심으로 하고 장축 반지름이 $a$, 단축 반지름이 $b$인 타원을 1사분에서 3차 Bezier curve을 이용해서 근사하려면 4개의 control
kipl.tistory.com
$$\mathbf {B}(t) = (1-t^3) \mathbf {P}_0 + 3t(1-t)^2 \mathbf {P}_1 + 3t^2 (1-t) \mathbf {P}_2 + t^3 \mathbf {P}_3 = \left(\begin {array}{c} a x(t) \\ b y(t) \end {array}\right) $$
$$ x(t) = 3k (1-t)^2 t + 3 (1-t) t^2 + t^3 \\ y(t) = x(1-t) , \quad 0 \le t \le 1$$
$k$ 값은 $t=1/2$일 때 $(a/\sqrt {2}, b/\sqrt {2})$을 통과하는 조건을 부여하여 정하면
$$ k = \frac {4}{3}(\sqrt {2}-1)= 0.5522847498...$$임을 알 수 있다.
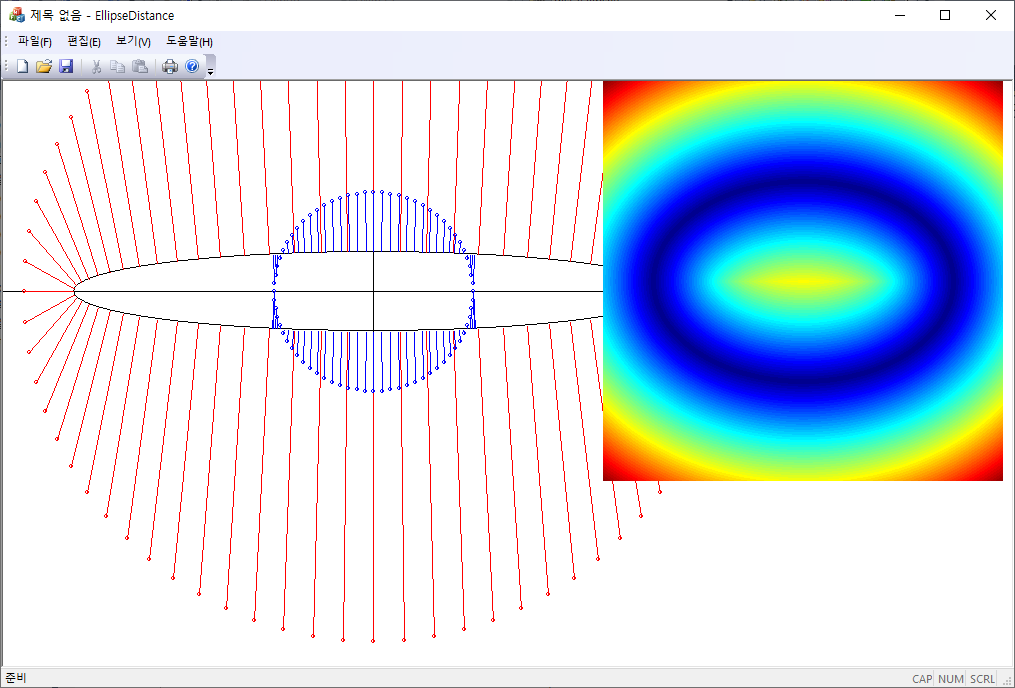
한 점 ${\bf P}=(p,q)$에서 베지어 곡선 위의 한 점 ${\bf B}(t)$까지의 거리가 최단거리가 되기 위해서는 다음 직교 조건
$$f(t)= ({\bf B}(t) - {\bf P})\cdot {\bf B}'(t) = 0 \\ f(t)=a^2x(t)x'(t)-b^2y(t)y'(t)-ap x'(t)-bqy'(t)=0$$
을 만족하는 근을 찾으면 된다. 풀어야 할 방정식이 5차이므로 직접적으로 근을 찾는 것은 불가능하므로 Newton-Raphson 방법을 사용하도록하자. 앞선 정확한 거리 계산에서와는 달리 초기 $t$ 값 설정에 민감하게 의존하지 않는다.
//cubic bezier_x: P0(0, 1), P1(k, 1),P2(1, k), P3(1, 0);
double B(double t) { //t in [0:1]
const double k = 4.*(sqrt(2.)-1)/3;
return t*(3*k + t*(3 - 6*k + (-2 + 3*k)*t));
}
// derivative of B(t);
double DB(double t) {
const double k = 4.*(sqrt(2.)-1)/3;
return 3*k + t*(6 - 12*k + (-6 + 9*k)*t);
}
// derivative of DB(t);
double D2B(double t) {
const double k = 4.*(sqrt(2.)-1)/3;
return 6 - 12*k + (-12 + 18*k)*t;
}
// ellipse radii=(a, b);
double dist2EllipseBezier3(double p, double q, double a, double b,
double& xt, double& yt) {
if (a == b) return dist2Circle(p, q, a, xt, yt);
double x = fabs(p), y = fabs(q);
const double eps = 0.001 / max(a, b);
double t = 0.5; // mid
while (1) {
// Newton-Raphson;
double f = a*a*B(t)*DB(t)-b*b*B(1-t)*DB(1-t)-a*x*DB(t)+b*y*DB(1-t);
if (f == 0) break;
double df = a*a*(DB(t)*DB(t)+B(t)*D2B(t))+b*b*(DB(1-t)*DB(1-t)+B(1-t)*D2B(1-t))
-a*x*D2B(t)-b*y*D2B(1-t);
double dt = f / df;
t -= dt;
t = max(0, min(1, t));
if (abs(dt) < eps ) break;
}
xt = a * B(t); yt = b * B(1-t);
xt = p >= 0? xt: -xt;
yt = q >= 0? yt: -yt;
return hypot(p - xt, q - yt);
}
'Computational Geometry' 카테고리의 다른 글
| Why Cubic Splines? (9) | 2024.03.16 |
|---|---|
| Natural Cubic Spline (0) | 2024.03.11 |
| Distance from a Point to an Ellipse (0) | 2024.03.06 |
| Data Fitting with B-Spline Curves (0) | 2021.04.30 |
| Closest Pair of Points (0) | 2021.04.27 |









