곡선의 길이를 구하고자 하면 곡선을 따라 속력을 적분하면 된다. 곡선을 기술하는 벡터가
그러나 일반적으로 이 적분은 닫힌 형태로 주어지지 않으므로 Gauss-Legendre quadrature와 같은 수치 적분에 의존해서 그 값을 계산하여야 한다.
Bezier curve의 경우는 기하학적인 방법을 이용하여서 좀 더 간편하게 그 길이를 구할 수 있다. Bezier curve의 길이에 대한 간단한 근사는 현의 길이(
그러나 이 근사가 유효하기 위해서는 현의 길이와 control point 간의 거리의 합
의 차이가 충분히 작아야 한다. 만약에 이 두 길이의 차이기 정해진 임계값보다도 크면 Bezier curve를 둘로 분할해서 좌우 두 Bezier curve에 대해서 동일한 검사를 한다. 충분히 평탄한 경우는 위의 평균값으로 근사하고 그렇지 못한 경우는 충분히 평탄해질 때까지 분할하는 과정을 반복한다. 아래 코드는 3차 Bezier curve의 길이를 이 알고리즘을 이용해서 구하는 과정을 구현한 것이다.

#define DistL2(A, B) sqrt(((A).x-(B).x)*((A).x-(B).x) + ((A).y-(B).y)*((A).y-(B).y))
static void BezierSubDiv(CfPt Q[4], CfPt leftQ[4], CfPt rightQ[4]) {
CfPt T[4][4]; /* Triangle Matrix */
for (int j = 0; j < 4; ++j) T[0][j] = Q[j];
// de Casteljau divides and conquers at t = 0.5;
for (int i = 1; i < 4; ++i)
for (int j = 0 ; j <= 3 - i; ++j)
T[i][j] = (T[i - 1][j] + T[i - 1][j + 1]) / 2;
// left subdiv control points;
for (int j = 0; j < 4; ++j) leftQ[j] = T[j][0];
// right subdiv control points;
for (int j = 0; j < 4; ++j) rightQ[j] = T[3 - j][j];
}
void BezierLength(CfPt Q[4], double tol, double *length) {
CfPt leftQ[4], rightQ[4];
double controlLen = 0;
for (int i = 0; i < 3; ++i) controlLen += DistL2(Q[i], Q[i + 1]);
double cordLen = DistL2(Q[0], Q[3]);
// test flatness;
if (fabs(controlLen - cordLen) > tol) {
BezierSubDiv(Q, leftQ, rightQ); /* divide */
BezierLength(leftQ, tol, length); /* left side */
BezierLength(rightQ, tol, length); /* right side */
return;
}
*length = *length + (cordLen + controlLen) / 2 ;
return ;
}

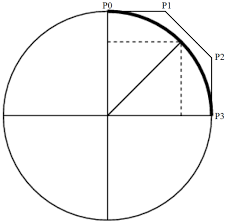
다음은 4분원의 길이를 위의 알고리즘을 이용해서 구하는 예제이다. 네 개의 control point는
이고,
int main() {
double k[4] = {0.5522847498, //touch at t = 0.5;
0.551915023, //min-deviation;
0.551778477, //match area;
0.551777131 //match length;
};
for (int i = 0; i < 4; i++)
printf("bezier length = %.8f\n", BezierLengthCircle(k[i]));
printf("exact length = %.8f\n", 2.0 * atan(1.));
return 0;
}
double BezierLengthCircle(double k) {
CfPt Q[4] = {{0, 1.}, {k, 1.}, {1., k}, {1., 0.}};
double len = 0;
double tol = 1.e-20;//
BezierLength(Q, tol, &len);
return len;
};

'Computational Geometry' 카테고리의 다른 글
| Convexity of Bezier Curve (0) | 2021.04.22 |
|---|---|
| De Casteljau's Algorithm (0) | 2021.04.22 |
| Bezier Curve Approximation of an Ellipse (0) | 2021.04.11 |
| Bezier Curve Approximation of a Circle (0) | 2021.04.10 |
| Bresenham's Line Algorithm (0) | 2021.04.07 |