Geometry & Recognition

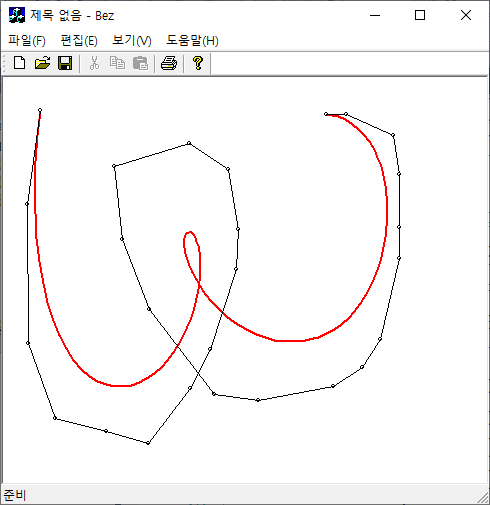
cubic Bezier 곡선은 네 개의 컨트롤 점 (${\mathbf{P}}_{\mathbf{0}}\mathbf{,}{\mathbf{P}}_{\mathbf{1}}\mathbf{,}{\mathbf{P}}_{\mathbf{2}}\mathbf{,}{\mathbf{P}}_{\mathbf{3}}$)이용해서 표현한다:

$$\begin{gathered} \mathbf{B}(t)=(1-t{)}^3{\mathbf{P}}_0+3(1-t{)}^{2}t{\mathbf{P}}_1+3(1-t)t^2{\mathbf{B}}_2+t^3{\mathbf{P}}_3.0\le t\le 1 \\ \mathbf{B}(0)={\mathbf{P}}_0,\mathbf{B}(1)={\mathbf{P}}_3 \end{gathered}$$

만약 곡선이 충분히 평탄하다면 굳이 삼차 다항식을 계수로 가지는 Bezier 곡선으로 표현할 필요가 없이${\mathbf{P}}_0$와  ${\mathbf{P}}_3$을 잇는 직선으로 근사하는 것이 여러모로 유리할 것이다. 그러면 Bezier 곡선의 평탄성을 어떻게 예측할 것인가? 이는 cubic Bezier 곡선 $\mathbf{B}(t)$와 시작점과 끝점을 연결하는 직선 $\mathbf{L}(t)=(1-t){\mathbf{P}}_0+t{\mathbf{P}}_3$와의 차이를 비교하므로 판단할 수 있다.

직선도 cubic Bezier 곡선 표현으로 할 수 있다. 시작점이 ${\mathbf{P}}_0$이고 끝점이 ${\mathbf{P}}_3$일 때 이 둘 사이를 3 등분하는 두 내분점 $(2{\mathbf{P}}_0+{\mathbf{P}}_3)/3$, $({\mathbf{P}}_0+2{\mathbf{P}}_3)/3$을 control point에 포함시키면,

$$\mathbf{L}(t)=(1-t{)}^3{\mathbf{P}}_0+(1-t{)}^{2}t(2{\mathbf{P}}_0+{\mathbf{P}}_3)+(1-t)t^2({\mathbf{P}}_0+2{\mathbf{P}}_3)+t^3{\mathbf{P}}_3$$

처럼 쓸 수 있다. Bezier 곡선과 직선의 차이를 구하면

$$\begin{array}{rl}\mathrm{\Delta }(t)& =|\mathbf{B}(t)-\mathbf{L}(t)|\\ & =|(1-t{)}^{2}t(3{\mathbf{P}}_1-2{\mathbf{P}}_0-{\mathbf{P}}_3)+(1-t)t^2(3{\mathbf{P}}_2-{\mathbf{P}}_0-2{\mathbf{P}}_3)|\\ & =3(1-t)t|(1-t)\mathbf{U}+t\mathbf{V}|,\\ \\ & \mathbf{U}={\mathbf{P}}_1-\frac{1}{3}(2{\mathbf{P}}_0+{\mathbf{P}}_3),\mathbf{V}={\mathbf{P}}_2-\frac{1}{3}({\mathbf{P}}_0+2{\mathbf{P}}_3)\end{array}$$

그런데 

$$\begin{gathered} \text{max}\{3(1-t)t\}=\frac{3}{4},0\le t\le 1, \\ \text{max}\{|(1-t)\mathbf{U}+t\mathbf{V}|\}=\text{max}\{|\mathbf{U}|,|\mathbf{V}|\} \end{gathered}$$

이므로 아래와 같은 벗어난 거리의 상한 값을 얻을 수 있다:

$$\mathrm{\Delta }(t)\le \frac{3}{4}\text{max}\{|\mathbf{U}|,|\mathbf{V}|\}$$

이 상한값이 주어진 임계값보다 작으면 3차 Bezier 곡선은 두 끝점을 잇는 직선으로 근사할 수 있다. 좀 더 기하학적으로 표현하면

$$|\mathbf{U}|={\mathbf{P}}_1\text{에서 왼쪽 3등분 내분점까지 거리}$$

$$|\mathbf{V}|={\mathbf{P}}_2\text{에서 오른쪽 3등분 내분점까지 거리}$$

이므로,

$$\mathrm{\Delta }(t)\le \frac{3}{4}\times (\text{control point와 3등분 내분점 간의 거리의 최댓값}).$$

Bezier 곡선은 control points $\{{\mathbf{P}}_i\}$의 선형 결합으로 주어진다:

$$\mathbf{B}(t)=\sum _{i=0}^n{B}_{i,n}(t){\mathbf{P}}_i,B_{i,n}(t)=\left(\begin{array}{c}n\\ i\end{array}\right)t^i(1-t{)}^{n-i}.$$

Bernstein 다항식 $B_{i,n}(t)$이 control points 선형 결합의 가중치를 역할을 하는데 0과 1 사이의 양의 실수 값을 가진다. 그리고 이들 가중치의 합은 1이다:

$$0\le B_{i,n}(t)\le 1,i=0,1,2,...n,0\le t\le 1$$

$$\sum _{i=0}^n{B}_{i,n}(t)=1$$

이는 Bezier 곡선이 control points가 만드는 convex region 내부에 있음을 의미한다. Bezier 곡선의 convexity 성질은 여러 좋은 특성을 준다.  몇 가지만 나열하면, 첫째가 Bezier 곡선은 항상 컨트롤 포인트의 convex hull 내에 놓이게 되므로 곡선의 제어 가능성을 보장한다. 둘째는 교차 여부를 쉽게 확인할 수 있다. 또한 culling을 가능하게 한다.

$n$ 차 Bezier 곡선은 두 개의 $(n-1)$ 차 Bezier 곡선의 선형보간으로 표현할 수 있다. Bezier 곡선은 Bernstein 다항식을 이용해서도 표현할 수도 있지만, 높은 찻수의 곡선일 때는 De Casteljau's Algorithm을 이용하는 것이 수치적으로 보다 안정적인 결과를 준다.

// De Casteljau's algorithm; recursive version; slow for larger deg;
double Bezier(int deg, double Q[], double t) {
   if (deg == 0) return Q[0];
   else if (deg == 1) return (1-t)*Q[0] + t*Q[1];
   else if (deg == 2) return (1-t)*((1-t)*Q[0] + t*Q[1]) + t*((1-t)*Q[1] + t*Q[2]);
   else return (1 - t) * Bezier(deg-1, &Q[0], t) + t * Bezier(deg-1, &Q[1], t);
}
// De Casteljau's algorithm(degree=n-1); 
// non-recursive. Bezier() modifies Q's;
double Bezier(int deg, double Q[], double t) {
    if (deg==0) return Q[0];
    else if (deg==1) return (1-t)*Q[0] + t*Q[1];
    else if (deg==2) return (1-t)*((1-t)*Q[0] + t*Q[1]) + t*((1-t)*Q[1] + t*Q[2]);
    
    for (int k = 0; k < deg; k++)
        for (int j = 0; j < (deg - k); j++)
            Q[j] = (1 - t) * Q[j] + t * Q[j + 1];
    return Q[0];
}
std::vector<CfPt> BezierCurve(const std::vector<CfPt> &cntls, const int segments) {
    std::vector<double> xp(cntls.size()), yp(cntls.size());
    std::vector<CfPt> curves(segments + 1);
    for (int i = 0; i <= segments; ++i) {
        double t = double(i) / segments;
        // clone control points; non-rec version modifies inputs;
        for (int k = cntls.size(); k-->0;) {
            xp[k] = cntls[k].x; yp[k] = cntls[k].y;
        }
        curves[i] = CfPt(Bezier(xp.size()-1, &xp[0], t), Bezier(yp.size()-1, &yp[0], t));
    }
    return curves;
};