Bezier Curve Approximation of a Circle

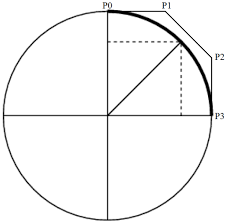
한 개의 Bezier 곡선을 이용해서 원을 표현할 수 없음은 잘 알려진 사실이다. 그럼 Bezier 곡선을 이용해서 얼마나 원(호)을 잘 근사할 수 있을까? 원점에 중심을 둔 반지름 1인 원의 1 사분면 원호가 3차 Bezier 곡선으로 얼마나 잘 표현되는지 알아보자. 3차 Bezier 곡선은 4개의 control point $\{{\mathbf{P}}_i|i=0,1,2,3\}$이 주어진 경우

$$\mathbf{B}(t)=(1-t^3){\mathbf{P}}_0+3t(1-t{)}^2{\mathbf{P}}_1+3t^2(1-t){\mathbf{P}}_2+t^3{\mathbf{P}}_3$$

으로 표현된다. 원호 근사에 필요한 control point의 위치는 다음 조건을 부여하면 얻을 수 있다.

(1) 시작점($t=0$)과 끝점($t=1$)은 원 위에 있어야 하므로

$$\mathbf{B}(t=0)=(0,1)\to {\mathbf{P}}_{\mathbf{0}}=(0,1),$$

$$\mathbf{B}(t=1)=(1,0)\to {\mathbf{P}}_{\mathbf{3}}=(1,0).$$

또 시작점과 끝점에서 접선이 원에도 접해야 하므로

$${\mathbf{B}}^{\prime }(t=0)\propto (1,0)\text{and}{\mathbf{B}}^{\prime }(t=1)\propto (0,-1)$$

에서 나머지 두 control point는 다음과 같이 쓸 수 있다:

$${\mathbf{P}}_1=(k,1),{\mathbf{P}}_2=(1,k).$$

그럼 $k$ 값은 어떻게 정할 수 있을까?

(2-1) Bezier 곡선의 중간지점이  원 위에 있도록 조건을 부여하면

$$\mathbf{B}(t=1/2)=(1/\sqrt{2},1/\sqrt{2})$$

을 얻고, 이를 이용하면

$$k=\frac{4}{3}(\sqrt{2}-1)=0.5522847498...$$

을 얻는다.

그럼 원에서 얼마나 벗어날까? 원 중심에서 거리를 차이를 구해보면 Bezier 곡선이 항상 원의 바깥으로 치우쳐 있음을 알 수 있다:

$$\mathrm{\Delta }(t)=||\mathbf{B}(t)||-1\ge 0$$ 

최대로 벗어나는 정도는 $t=(3\pm \sqrt{3})/6$일 때 ${\mathrm{\Delta }}_{\text{max}}=\frac{1}{3}\sqrt{\frac{71}{6}-2\sqrt{2}}-1=0.00027253...$이므로 대부분의 경우 크게 벗어남이 없는 원의 근사를 준다.

(2-2) $t=1/2$에서 Bezier 곡선이 원을 통과하는 조건 대신 원에서 벗어남을 최소로 하는 조건을 부여하면 더 좋은 근사를 얻을 수 있다:

$$k=\text{argmin}|\mathrm{\Delta }{|}_{\text{max}}$$

이 경우  Bezier 곡선은 원의 바깥에 놓이지 않고 교차하게 된다. $t=1/2$에서 최솟값, $t=\frac{1}{2}(1\pm \frac{\sqrt{3k^2+20k-12}}{2-3k})$일 때 최댓값을 가지는데, 두 값의 절댓값이 같게 되려면(closed form이 없다)

$$k=0.551915023...$$

을 선택해야 하고, 이때 벗어남의 최댓값은 $|\mathrm{\Delta }{|}_{\text{max}}=0.00019607...$이므로 더 좋은 근사가 된다.

 

(2-3) 또 다른 제한조건은 없을까? Bezier 곡선이 만드는 면적이 사분원의 면적을 표현하도록 제한을 가하는 경우:

$$\frac{\pi }{4}={\int }_0^1\frac{1}{2}(B_y{B}_x^{\prime }-B_x{B}_y^{\prime })dt$$

$$={\int }_0^1(-\frac{3}{2}(3k^2(t-1{)}^2{t}^2+k(-2t^4+4t^3-6t^2+4t-1)+2(t-1)t))dt$$

$$=\frac{1}{2}+\frac{3k}{5}-\frac{3k^2}{20}$$ 에서 

$$k=2-\sqrt{\frac{22-5\pi }{3}}=0.551778477...$$

이다. 이 경우 면적은 같으나 벗어남 오차는 $t=1/2$일 때

$$|\mathrm{\Delta }{|}_{\text{max}}=\frac{1}{8}\sqrt{332-40\sqrt{66-15\pi }-30\pi }-1=0.00026849...$$

로 주어지는데, 중심을 지나는 경우보다는 벗어남이 작지만 최소는 아니다.

(2-4) Bezier 곡선의 길이가 원주가 되는 제한조건을 걸 수도 있다:

$$\frac{\pi }{2}={\int }_0^1\sqrt{(B_x^{\prime }{)}^2+(B_y^{\prime }{)}^2}dt.$$

그런데 우측 적분이 closed form으로 주어지지 않는다. 때문에 $k$ 값을 구하기 위해서 전적으로 numerical method에 의존해야 되는데,  그 결과만 쓰면

$$k=0.551777131...$$