화면이나 그림에서 직선을 그리려면 직선의 방정식을 만족하는 모든 픽셀들을 찾으면 된다. 하지만 픽셀의 위치는 연속적인 값이 아니라 이산적이므로 그림에 그려진 직선을 구성하는 픽셀은 그 직선을 표현을 하는 식이 주는 값에 가장 가까운 정수를 찾아서 그린 것이다. 직선을 그리기 위해서 실수 연산을 한 후 정수로 반올림하는 과정이 들어가게 된다.
Bresenham 알고리즘은 평면 위의 두 점 $(x_0, y_0), (x_1, y_1)$을 연결하는 직선을 정수 연산만을 사용하여 그릴 수 있음을 보여준다. 직선의 방정식은 $y = mx +b$의 형태로 표현이 되고, 두 점이 주어지는 경우 기울기는 $m = \frac {y_1 - y_0}{x_1 - x_0} = \frac {\Delta y}{\Delta x}$, $y-$절편은 $b =y_0 - m x_0$로 얻을 수 있다. 직선의 기울기가 1보다 크면 $x$와 $x+1$에서 변할 때 종속변수 $y$값의 차이가 커지므로 선이 연속적으로 그려지지 않게 보인다. 이 경우 $y$를 독립변수로 사용하면 되고, 기울기가 음수면 시작과 끝을 바꾸면 된다. 따라서 기울기가 $0\le m \le 1$인 경우만 살펴보면 충분하다.
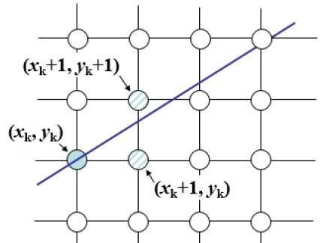
이제, $(x_k, y_k)$ 위치에서 직선의 픽셀이 정해진 경우, $x_{k+1}= x_k + 1$에서 직선식의 값 $y =m (x_k + 1) + b$는 어떤 정수 값으로 대체되어야 하는가? 기울기가 1보다 작으므로 $y$는 구간 $[y_k, y_k +1]$에서 값을 취한다. 즉, 오른쪽 옆이나 오른쪽 위 픽셀에 점을 찍어야 한다. 수식으로는 구간의 아래($d_{lower}$)와 위쪽($d_{upper}$)과의 차이를 비교하여 작은 쪽으로 결정하면 된다:
$$ d_{lower} = y - y_k = m(x_k + 1) +b - y_k$$
$$ d_{upper} = (y_k + 1) - y = y_k + 1 - m (x_k + 1) -b$$
이 과정을 실수 연산 없이 판별하는 방법을 알아내자. $d_{lower}$와 $d_{upper}$의 차이는
$$ d_{lower} - d_{upper} = 2m (x_k + 1) - 2 y_k + 2b -1$$
로 표현되고, 나눗셈을 하지 않기 위해서 $\Delta x$을 곱한 값을 discriminator로 사용하자:
$$p_k = \Delta x(d_{lower} - d_{upper} )= 2 \Delta y (x_k + 1) - 2 \Delta x y_k + \Delta x (2b-1)$$
의 꼴로 표현되므로 직선의 정보($\Delta x, \Delta y$)와 현재 점을 찍은 픽셀($x_k, y_k$)을 알면 다음번에 점을 찍을 픽셀을 정수 연산만 가지고 판별할 수 있는 장점이 있다. $k+1$일 때 판별식이
$$ p_{k+1} = 2 \Delta y (x_k + 1) - 2 \Delta x y_{k+1} + \Delta x (2b-1)$$
이므로 다음과 같은 recursion relation을 만족한다:
$$p_{k+1} = p_k + 2\Delta y - 2\Delta x (y_{k+1} - y_k) \\ p_0 = 2\Delta y - \Delta x$$
이를 이용하면 시작 픽셀 $(x_0, y_0)$에서 $p_0 = 2\Delta y - \Delta x$을 계산하여 0보다 작지 않으면 $(x_k + 1, y_k+1)$ 픽셀에 점을 찍고, 그다음 점찍을 픽셀은 $p_{k+1} = p_k + 2\Delta y - 2\Delta x$을 이용해서 판별한다. $p_0 < 0$ 이면 ($x_k +1, y_k$) 픽셀에 점을 찍고, 그다음 점을 찍을 픽셀은 $p_{k+1}= p_k + 2\Delta y$을 계산하여 판별한다.
void BresenhamLine(int x1, int y1, int x2, int y2, DWORD color) {
int dx = x2 - x1 ;
int incx = 1;
if (dx < 0) {
dx = -dx;
incx = -1;
}
int dy = y2 - y1;
int incy = 1;
if (dy < 0) {
dy = -dy;
incy = -1;
}
setPixel(x1, y1,color);
if (dx > dy) {
int p = (dy << 1) - dx;
while (x1 != x2) {
if (p >= 0) {
y1 += incy;
p -= (dx << 1);
}
x1 += incx;
p += (dy << 1);
setPixel(x1, y1, color);
}
} else {
int p = (dx << 1) - dy;
while (y1 != y2) {
if (p >= 0) {
x1 += incx;
p -= (dy << 1);
}
y1 += incy;
p += (dx << 1);
setPixel(x1, y1, color);
}
}
};'Computational Geometry' 카테고리의 다른 글
| Bezier Curve Approximation of an Ellipse (0) | 2021.04.11 |
|---|---|
| Bezier Curve Approximation of a Circle (0) | 2021.04.10 |
| Rotating Calipers (3) | 2021.03.31 |
| Convex Hull Peeling (0) | 2021.03.29 |
| Graham Scan (0) | 2021.03.28 |



