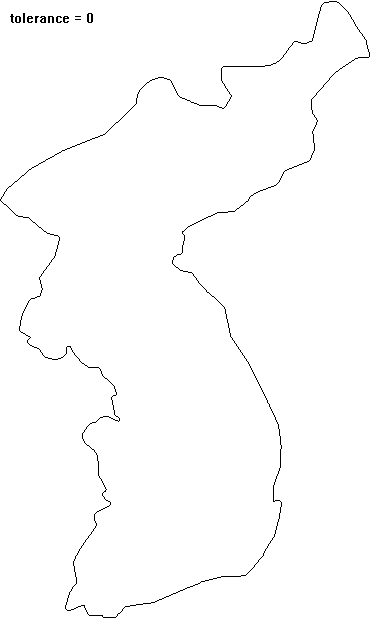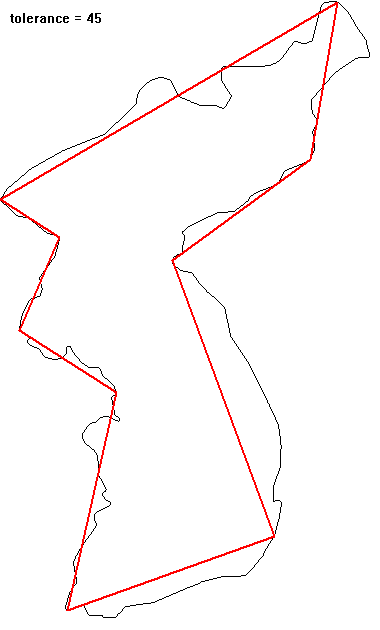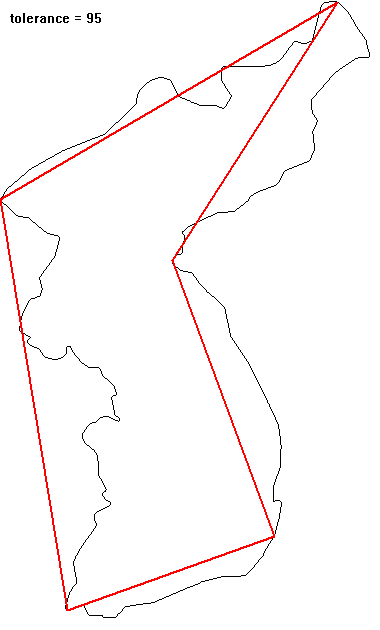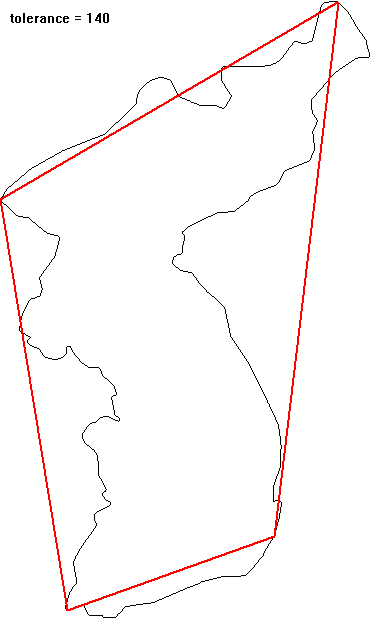
영상에서 추출한 객체(object)의 경계선은 객체의 모양에 대한 많은 정보를 담고 있지만, 어떤 경우에는 불필요하게 많은 정보가 될 수도 있다. 이 경우 원래의 경계를 충분히 닮은 다각형으로 간략화하여서 불필요한 정보를 제거할 수 있다. 이 다각형으로의 근사가 물체의 경계를 얼마나 제대로 표현할 수 있는지에 대한 기준이 있어야 한다. $N$개의 점 $\{(x_i, y_i) | i = 1,... ,N\}$으로 표현된 경계가 있다고 하자. 가장 단순한 근사는 가장 멀리 떨어진 두 점($A, B$)으로 만들어진 선분일 것이다(선분의 길이가 대략적인 물체의 크기를 주고, 선분 방향이 물체의 orientation을 알려준다). 이 선분을 기준으로 다시 가장 멀리 떨어진 점($C$)을 찾아서 일정 거리 이상 떨어져 있으면 꼭짓점으로 추가하여 두 개의 선분으로 분할한다. 두 개의 선분에 대해서 동일한 분할 작업을 재귀적으로 반복하므로 좀 더 정밀하게 물체를 표현하는 다각형을 찾을 수 있다. 선분에서 가장 멀리 떨어진 지점이 기준 거리 이내이면 분할을 멈춘다. 닫힌 다각형 근사일 때는 시작점 = 끝점으로 조건을 부여하면 된다.
** open polyline으로 우리나라 경계를 단순화시키는 예: top-right 쪽이 시작과 끝이므로 simplication 과정에서 변화지 않는다.
// distance square from P to the line segment AB ;
double pt2SegDist2(CPoint P, CPoint A, CPoint B) ;
// P에서 두 점 A, B을 연결하는 선분까지 거리
double pt2SegDist2(CPoint P, CPoint A, CPoint B) {
double dx = B.x - A.x, dy = B.y - A.y ;
double lenAB2 = dx * dx + dy * dy ;
double du = P.x - A.x, dv = P.y - A.y ;
if (lenAB2 == 0.) return du * du + dv * dv;
double dot = dx * du + dy * dv ;
if (dot <= 0.) return du * du + dv * dv;
else if (dot >= lenAB2) {
du = P.x - B.x; dv = P.y - B.y;
return du * du + dv * dv;
} else {
double slash = du * dy - dv * dx ;
return slash * slash / lenAB2;
}
};// recursive Douglas-Peucker 알고리즘;
void DouglasPeucker(double tol, std::vector<CPoint>& vtx, int start, int end,
std::vector<bool>& mark) {
if (end <= start + 1) return; //종료 조건;
// vtx[start] to vtx[end]을 잇는 선분을 기준으로 분할점을 찾음;
int break_id = start; // 선분에서 가장 먼 꼭짓점;
double maxdist2 = 0;
const double tolsq = tol * tol;
for (int i = start + 1; i < end; i++) {
double dist2 = pt2SegDist2(vtx[i], vtx[start], vtx[end]);
if (dist2 <= maxdist2) continue;
break_id = i;
maxdist2 = dist2;
}
if (maxdist2 > tolsq) { // 가장 먼 꼭짓점까지 거리가 임계값을 넘으면 => 분할;
mark[break] = true; // vtx[break_id]를 유지;
// vtx[break_id] 기준으로 좌/우 polyline을 분할시도;
DouglasPeucker(tol, vtx, start, break_id, mark);
DouglasPeucker(tol, vtx, break_id, end, mark);
}
};// driver routine;
std::vector<CPoint> polySimplify(const double tol, const std::vector<CPoint> &V) {
if (V.size() <= 2) return V;
std::vector<bool> mark(V.size(), false); // 꼭짓점 마킹용 버퍼;
// 알고리즘 호출 전에 너무 붙어있는 꼭짓점을 제거하면 보다 빠르게 동작;
// 폐곡선이 아닌 경우 처음,끝은 marking;
// 폐곡선은 가장 멀리 떨어진 두점중 하나만 해도 충분;
mark.front() = mark.back() = true;
DouglasPeucker( tol, V, 0, V.size()-1, mark );
// save marked vertices;
std::vector<CPoint> decimated;
for (int i = 0; i < V.size(); i++)
if (mark[i]) decimated.push_back(V[i]);
return decimated;
}nonrecursive version:
// nonrecursive version;
std::vector<CPoint> DouglasPeucker_nonrec(const double tol, const std::vector<CPoint>& points) {
if (points.size() <= 2) return std::vector<CPoint> (); //null_vector;
double tol2 = tol * tol; //squaring tolerance;
// 미리 가까이 충분히 가까이 있는 꼭지점은 제거하면 더 빨라짐;
std::vector<CPoint> vt;
vt.push_back(points.front()) ; // start at the beginning;
for (int i = 1, pv = 0; i < points.size(); i++) {
int dx = points[i].x - points[pv].x, dy = points[i].y - points[pv].y;
double dist2 = dx * dx + dy * dy ;
if (dist2 < tol2) continue;
vt.push_back(points[i]);
pv = i; // 다시 거리를 재는 기준점;
}
if (vt.back()!=points.back()) vt.push_back(points.back()); // finish at the end
points.swap(vt);
//
std::vector<bool> mark(points.size(), false); // vertices marking
std::vector<int> stack(points.size()); // 분할된 라인 처음-끝 저장;
// 폐곡선이 아닌 경우 처음,끝은 marking;
// 폐곡선은 가장 멀리 떨어진 두점 중 하나만 해도 충분
mark.front() = mark.back() = true;
int top = -1;
// 분할 해야할 폴리라인의 양끝점을 스택에 넣음;
stack[++top] = 0;
stack[++top] = points.size() - 1;
while (top >= 0) {
// 분할을 시도할 구간의 두 끝점을 꺼냄;
int end = stack[top--];
int start = stack[top--];
// 최대로 멀리 떨어진 점;
double max_distance2 = 0;
int break_id = -1;
for (int i = start + 1; i < end; i++) {
double dsq = pt2SegDist2(points[i], points[start], points[end]);
if (dsq > max_distance2) {
max_distance2 = dsq;
break_id = i;
}
}
// 주어진 임계값 이상 떨어졌으면 꼭지점을 유지하도록 표시;
if (max_distance2 > tol2) {
mark[break_id] = true;
// 주어진 꼭지점을 기준으로 양쪽을 다시 검사하기 위해 스택에 쌓음;
stack[++top] = start;
stack[++top] = break_id;
stack[++top] = break_id;
stack[++top] = end;
}
}
// marking 된 꼭지점을 출력;
std::vector<CPoint> decimated;
for (int i = 0; i < points.size(); i++)
if (mark[i]) decimated.push_back(points[i]);
return decimated;
}'Computational Geometry' 카테고리의 다른 글
| Brute Force Convex Hull Algorithm (0) | 2012.09.06 |
|---|---|
| Curvature of a Curve (0) | 2012.08.07 |
| Inside Quadrilateral, Inside Triangle (0) | 2012.01.18 |
| 3개의 숫자 중에서 가장 큰 것은 (1) | 2012.01.17 |
| 소금 호수에 생긴 보로노이 다이어그램 (1) | 2010.11.06 |



