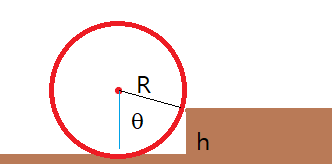
볼링공(반지름: $R$, 회전관성: $\frac{2}{5} mR^2$)이 굴러가다가 턱에 부딪치는 경우를 보자. 충돌이 비탄성적이라면 공은 턱(높이: $h$)을 기준으로 회전해서 턱 위로 올라갈 수 있다. 물론 부딪치기 직전 속도가 너무 작으면 오를 수 없고, 너무 크면 위로 튄다. 어떤 조건일 때 튀지 않고 턱 위로 올라갈 수 있을까?
1. 충돌 전후로 턱에 대한 각운동량이 보존되므로 충돌 직후 각속도 $\omega$는 충돌 전 속도($v_0$)를 알면 구할 수 있다.
$$I \left( \frac{v_0}{R} \right) + mv _0(R-h) = (I + mR^2) \omega$$
$$ \to ~~\omega= \left( 1 - \frac{5h}{7R}\right) \frac{v_0}{R}$$
2. 역학적 에너지 보존을 이용하면 공이 턱에 완전히 올라서기 위해서는 충돌 직후 각속도 $\omega$가 일정한 크기 이상이어야 한다:
$$\frac{1}{2} (I+ mR^2) \omega^2 \ge mgh$$
$$ \to ~~R \omega \ge \sqrt{\frac{10}{7 }gh}$$
$$\text{or}~~ v_0 \ge\frac{1}{1- 5h/7R} \sqrt{\frac{10}{7} gh}$$
728x90
'Physics > 역학' 카테고리의 다른 글
| 실린더가 움직이는 방향은? (0) | 2022.01.06 |
|---|---|
| 얼마나 기울여야 하는가? (0) | 2021.05.23 |
| 새는 비행기를 순간적으로 정지시켰는가? (0) | 2021.02.04 |
| 공기 저항이 있을 때 (2) (0) | 2021.01.29 |
| 움직일 수 있는 경사면을 내려왔을 때 속력은? (0) | 2021.01.22 |



