Geometry & Recognition

표준형 타원

$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$$

의 두 주축에 대한 central moment (moment of inertia)는 각각

$$ \mu_{20} = \frac{\pi}{4} a^3 b, \quad \mu_{02} = \frac{\pi}{4} ab^3$$ 

으로 주어짐은 쉽게 계산할 수 있다. 그런데 타원의 면적인 0차 central moment가 $\mu_{00}= \pi ab$이므로 normalized central moment (위치의 분산을 의미한다)는 각각

$$\tilde\mu_{20} = \frac{\mu_{20}}{\mu_{00}} = \frac{1}{4}a^2, \quad  \tilde\mu_{02} = \frac{\mu_{02}}{\mu_{00}} = \frac{1}{4}b^2$$

따라서 장축과 단축의 반지름은 주축에 대한 2차 normalized central moment을 구하면 얻을 수 있다.

기울어진 타원의 경우는 $\tilde\mu_{pq}$가 픽셀의 분포를 알려주므로 이를 이용한 covariance 행렬의 고유값을 구하면 장축과 단축의 반지름을 알 수 있고, 기울어진 정도도 알 수 있다. 공변행렬

$$ \Sigma = \left( \begin{array}{cc} \tilde\mu_{20} & \tilde\mu_{11} \\ \tilde\mu_{11} & \tilde\mu_{02} \end{array} \right)$$

의 두 고윳값은

$$ \lambda_1 = \frac{1}{2}\left( \tilde\mu_{20}+ \tilde\mu_{02} + \sqrt{ (\tilde\mu_{20} - \tilde\mu_{02})^2 + 4 \tilde\mu_{11}^2} \right),$$

$$ \lambda_2 = \frac{1}{2}\left( \tilde\mu_{20}+ \tilde\mu_{02} - \sqrt{ (\tilde\mu_{20} - \tilde\mu_{02})^2 + 4 \tilde\mu_{11}^2} \right).$$

따라서 기울어진 타원의 장축과 단축의 반지름, 그리고 회전각은

$$ a = 2\sqrt{ \lambda_1}, \quad b = 2\sqrt{ \lambda_2}, \quad \tan(2\theta)=\frac{2 \tilde\mu_{11}}{ \tilde\mu_{20}-\tilde\mu_{02}   }$$

로 주어지므로 회전된 좌표계 $(u, v)$에서 타원의 방정식은

$$ \frac{ u^2 }{4 \lambda_1} + \frac{v^2 }{4\lambda_2} = 1$$

로 쓰인다. 

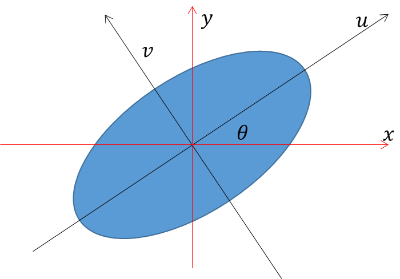
다시 원 좌표계 $(x, y)$로 돌아가기 위해서 (물론 질량중심이 원점인 좌표계이다)

$$ u =  \cos \theta x+  \sin \theta y, \quad v = -\sin \theta x + \cos \theta y$$

를 대입하면 타원을 2차식 형태

$$ A x^2 + 2B xy + C y^2 = 1$$

로 쓸 수 있는데, 그 계수는

$$ A= \frac{1}{8}\left( \frac{1}{\lambda_1} + \frac{1}{\lambda_2} +\Big( \frac{1}{\lambda_1} - \frac{1}{\lambda_2} \Big) \cos (2\theta) \right)=\frac{\tilde\mu_{02}}{ 4(\tilde\mu_{20}\tilde\mu_{02}-\tilde\mu_{11}^2 )} $$

$$ C= \frac{1}{8}\left( \frac{1}{\lambda_1} + \frac{1}{\lambda_2} -\Big( \frac{1}{\lambda_1} - \frac{1}{\lambda_2} \Big) \cos (2\theta) \right)=\frac{\tilde\mu_{20}}{ 4(\tilde\mu_{20}\tilde\mu_{02}-\tilde\mu_{11}^2 )} $$

$$ B= \frac{1}{8}\left( \frac{1}{\lambda_1} - \frac{1}{\lambda_2} \right)\sin (2\theta)=\frac{-\tilde\mu_{11}}{ 4(\tilde\mu_{20}\tilde\mu_{02}-\tilde\mu_{11}^2 )} $$

로 주어진다. 주어진 object의 normalized central moment를 구하면 타원 fitting에 대한 정보를 구할 수 있음을 보였다.

영상에 담고 있는 object을 간단히 근사를 할 때 타원으로 많이 기술한다(e.g: head tracking). 타원으로 기술하면 장축의 방향으로 object의 기울어진 방향을, 장축과 단축의 길이로 object의 크기를 가늠할 수 있다. object의 픽셀 분포에서 형상에 대한 정보는 2차 moment를 계산해서 얻을 수 있다. 이는 타원이 2차 곡선이기 때문에 가능하다. 그리고 질량중심을 원점으로 잡으면 2차 central moment를 계산해야 한다. 그런데 통계적인 의미를 부여하기 위해서는 central moment를 object의 픽셀로 나눈 normalized central moment로 구성한 covariance matrix를 사용하면 된다.

$$\Sigma = \left(\begin{array}{cc} \tilde\mu_{20} &  \tilde\mu_{11} \\ \tilde\mu_{11} & \tilde\mu_{02} \end{array} \right), \quad\quad\tilde\mu_{pq} \equiv \frac{\mu_{pq}}{\mu_{00}},  \quad (p+q=2)$$ 

(Note: $\mu_{00}$로 정규화를 하지 않더라도 문제는 없다).

$\Sigma$는 영상에서 object pixel의 $x$ 뱡향 분산($\mu_{20}$: $x$축에 대한 회전관성), $y$ 방향 분산($\mu_{02}$: $y$축에 대한 회전관성), $x$-$y$의 correlation을 나타낸다. $\Sigma$가 대칭행렬이므로 두 개의 음이 아닌 고윳값을 가진다. 

\begin{gather} \lambda_1 = \frac{\tilde\mu_{20} + \tilde\mu_{02}}{2} + \frac{ \sqrt{(\tilde\mu_{20} - \tilde\mu_{02})^2 + 4\tilde\mu_{11}^2 } }{2}, \\  \lambda_2 = \frac{\tilde\mu_{20} + \tilde\mu_{02}}{2} - \frac{ \sqrt{(\tilde\mu_{20} - \tilde\mu_{02})^2 + 4\tilde\mu_{11}^2 } }{2}\end{gather}

큰 고유값에 해당하는 고유벡터의 방향이 타원의 장축 방향에 해당하고 (픽셀 변동이 심하므로) , 작은 고윳값의 고유벡터 방향은 단축 방향이다. 그리고 고윳값은 각각 장축과 단축의 반지름의 제곱에 비례한다($\tilde\mu_{pq}$는 단위가 거리 제곱이다). object의 orientation인 타원의 장축 방향은 

$$ \theta = \frac{1}{2} \tan^{-1} \Big( \frac{   2\tilde\mu_{11} }{\tilde\mu_{20} - \tilde\mu_{02}}\Big)= \frac{1}{2} \tan^{-1} \Big( \frac{   2\mu_{11} }{\mu_{20} - \mu_{02}}\Big) $$

로 계산된다. (https://kipl.tistory.com/58)

타원의 orientation 각도를 구했으므로 두 주축을 나타내는 단위벡터는

$$\text{major axis: }(\cos \theta, \sin \theta), \quad \text{minor axis: }(-\sin\theta, \cos \theta)$$

로 쓸 수 있다. 그리고 이 두 축에 대한 object의 회전관성은 정의에 의해서 다음 식으로 구할 수 있다: $(\bar{x}, \bar{y})=\text{center of mass}$

\begin{align}\text{major axis:} ~I_\text{min} &= \sum_{(x, y )\in \text{object}} | - (x-\bar{x})\sin \theta + (y - \bar{y})\cos \theta |^2 \\ &=\frac{\mu_{20}+\mu_{02}}{2} -\frac{\mu_{20} - \mu_{02}}{2} \cos (2\theta)-  \mu_{11} \sin(2\theta)\end{align}

\begin{align}\text{minor axis:} ~I_\text{max} &= \sum_{(x, y)\in \text{object}} | (x-\bar{x}) \cos \theta + (y - \bar{y}) \sin \theta|^2 \\&= \frac{\mu_{20}+\mu_{02}}{2}+\frac{\mu_{20}-\mu_{02}}{2}\cos (2\theta)+ \mu_{11}\sin(2\theta)\end{align}

(note: object의 orientation 각은 $I_\text{min}$을 최소화시키는 값이다)

표준 타원의 장축 반지름이 $a$고 단축 반지름이 $b$일 때 ($x^2/a^2 + y^2/b^2 =1$) 2차 central moment(회전관성)는 간단한 계산에 의해서

$$\mu_{20}^\text{(e)} = \frac{\pi}{4} a^3 b, \quad \mu_{02}^\text{(e)} = \frac{\pi}{4} ab^3,\quad \mu_{11}^\text{(e)}= 0$$

으로 구해짐을 알 수 있다.

주어진 타원이 object을 잘 피팅하려면 타원의 두 축에 대한 회전관성이 각각 object의 주축에 대한  회전관성과 같은 값을 가져야 할 것이다:

$$ I_\text{min} = \mu_{20}^\text{(e)}, \quad I_\text{max} =\mu_{02}^\text{(e)}$$

이 두 식을 풀면 타원의 장축과 단축의 반지름을 구할 수 있다. 

$$a = \Big( \frac{4}{\pi}\Big)^{1/4} \Big( \frac{I_\text{max}^3}{I_\text{min}}\Big)^{1/8}, \quad b = \Big( \frac{4}{\pi}\Big)^{1/4} \Big( \frac{I_\text{min}^3}{I_\text{max}}\Big)^{1/8}$$

보통 object을 타원 피팅할 때 윤곽선 정보를 이용하는데, 이 방법은 윤곽선을 추출할 필요가 없어서 편리하다. 단 내부에 빈 곳이 있는 object의 경우 회전관성을 감소시키므로 좋은 결과를 기대할 수 없다. 영상이 다수의 object를 담고 있을 때는 connected component labeling을 한 후 각각의 component에 대해서 fitting을 수행하면 된다.

void getEllipse(CRaster& raster) {
    const double four_pi = 1.0 / atan(1.0);
    CSize sz = raster.GetSize();
    double xsum = 0, ysum = 0;
    double x2sum = 0, y2sum = 0, xysum = 0;
    int count = 0;
    for (int y = 0; y < sz.cy; y++) {
        BYTE *p = (BYTE *)raster.GetLinePtr(y);
        for (int x = 0; x < sz.cx; x++) {
            if (*p++) {
                count++;
                xsum += x;      ysum += y;
                x2sum += x * x; y2sum += y * y; 
                xysum += x * y;
            }
        }
    }
    if (!count) return;
    double xm = xsum / count;
    double ym = ysum / count;
    double m20 = x2sum - xm * xm * count;
    double m02 = y2sum - ym * ym * count;
    double m11 = xysum - xm * ym * count;
    double theta2 = atan2(2 * m11, m20 - m02);
    double ct = cos(theta2), st = sin(theta2);
    double Imin = 0.5 * (m20 + m02) - 0.5 * (m20 - m02) * ct - m11 * st;
    double Imax = 0.5 * (m20 + m02) + 0.5 * (m20 - m02) * ct + m11 * st;
    double major = pow(four_pi, 0.25) * pow(Imax * Imax * Imax / Imin, 0.125);
    double minor = pow(four_pi, 0.25) * pow(Imin * Imin * Imin / Imax, 0.125);
    drawEllipse(raster, mx, my, major, minor, theta2 / 2);
}