$$I=\text{Pr} \int_{-1}^{1} \left( \frac{ 1+x}{1-x}\right)^{1/2} \frac{dx}{(2-x)x}$$
contour 적분을 이용해서 이를 구하기 위해 다음의 복소함수를 고려한다.
$$f(z) = \left( \frac{1+z}{1-z}\right)^{1/2} \frac{1}{(2-z)z}$$
$f(z)$는 $z=\pm 1$이 branch point 이고 $z=0, 2$에서 simple pole을 가진다. Branch cut을 그림처럼 두 지점을 연결하는 선분으로 잡으면 $z+1$과 $1-z$의 위상을 $$-\pi \le \theta \le \pi, \quad 0 \le \arg(1-z) \le 2\pi$$로 선택할 수 있다.
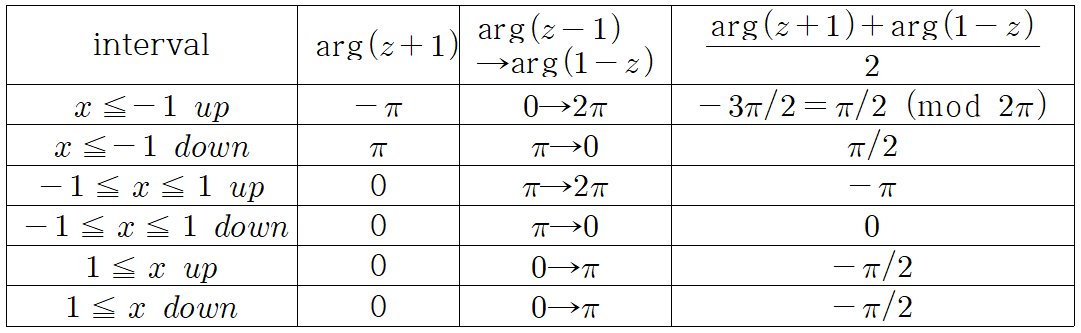
Branch cut과 pole을 감싸는 그림과 같은 경로에 대해서 선적분은 다음과 같이 나누어진다.
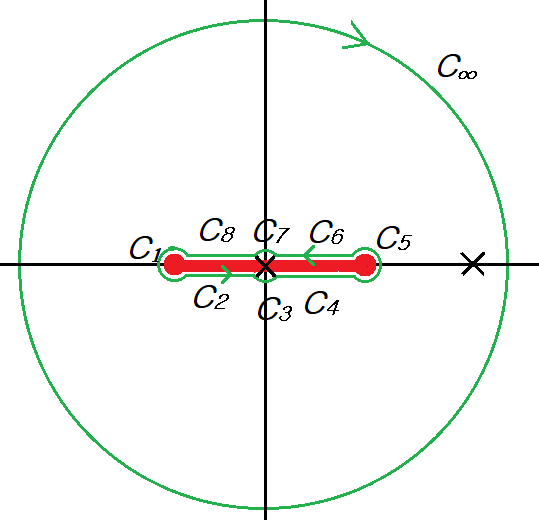
$$ \sum_{k} \int_{C_k} f(z) dz + \int_{C_\infty} f(z) dz =- 2\pi i \times \text{Res}(z=2)$$
$C_\infty$에서 $$\int_{C_\infty} f(z)dz = O(1/R) \rightarrow 0$$
$C_1$에 대해서 $z+1=\epsilon e^{i \theta} ~(\theta: -\pi \rightarrow \pi)$, $z-1= 2 e^{i \pi}$이므로
$$ \int_{C_1} f(z) dz \sim O(\sqrt{\epsilon} \epsilon ) \rightarrow 0 $$
$C_5$에 대해서, $z-1=\epsilon e^{i \theta}~(\theta:0 \to 2\pi)$, $z+1= 2e^{0i},~(\theta: 0 \to 2\pi)$이므로
$$ \int_{C_5} f(z) dz \sim O(\sqrt{\epsilon}) \rightarrow 0 $$
$C_7$에서는 $z=\epsilon e^{i \theta}~(\theta:0\to\pi)$, $z+1=e^{i0}$, $z-1=e^{i \pi}\to 1-z=e^{i 2\pi} $이고, $C_3$에서는 $z=\epsilon e^{i \theta}~(\theta: \pi \to 2\pi) $, $z+1= e^{i 0}$, $z-1=e^{i \pi}\to 1-z=(1-x) e^{i0}$이므로
$$\int_{C_3} f(z)dz = \frac{1}{2}\int_{\pi}^{2\pi}\frac{ i \epsilon e^{i \theta} d\theta}{\epsilon e^{i \theta}}=\frac{i \pi }{2} \\ \int_{C_7} f(z)dz = -\frac{1}{2}\int_0^{\pi} \frac{i \epsilon e^{i\theta} d\theta}{\epsilon e^{i\theta}}=-\frac{i \pi }{2} \\ \to \int_{C_3+C_7} f(z)dz= 0$$
$C_2$와 $C_4$에서는 $$z+1=(1+x)e^{i 0} ~~(x: -1 \to 1)\\ z-1= (1-x) e^{i \pi} \to 1-z=(1-x) e^{ i 0} \\ \to ~\sqrt{\frac{1+z}{1-z}} = \sqrt{\frac{1+x}{1-x}}$$
$$\int_{C_2 + C_4} = \int_{-1}^{1} \sqrt{ \frac{1+x}{1-x}} \frac{dx}{(2-x)x}= I$$
$C_6$와 $C_8$에서는 $$z+1=(1+x)e^{0i}~~(x:1\to -1) \\ z-1= (1-x) e^{i\pi} \to 1-z= (1-x) e^{i 2\pi} \\ \to ~\sqrt{\frac{1+z }{1-z}} = \sqrt{\frac{1+x}{1-x}}\frac{1}{e^{i\pi}} = -\sqrt{\frac{1+x}{1-x}}$$이므로 $$\int_{C_6+C_8} = -\int_{1}^{-1} \sqrt{\frac{1+x}{1-x}} \frac{dx}{(2-x)x} = I$$ $z=2$에서 residue을 계산하면 $$ \text{Res} (z=2) = -\frac{\sqrt{3}}{i} \frac{1}{2}=\frac{\sqrt{3}}{2i}$$ 따라서 $$ 2I = 2\pi i\times \frac{\sqrt{3}}{2i} \longrightarrow I= \frac{\pi \sqrt{3} }{2}$$
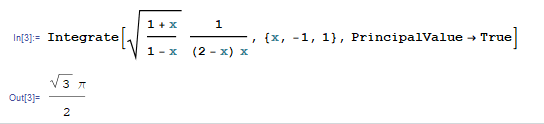
'Mathematics' 카테고리의 다른 글
| Mean distance between two randomly chosen points in unit square (0) | 2022.01.28 |
|---|---|
| Catenary (0) | 2022.01.14 |
| Integration along a branch cut-013 (0) | 2021.12.22 |
| Integration along a branch cut-012 (0) | 2021.01.05 |
| Integration along a branch cut-011 (0) | 2021.01.04 |




