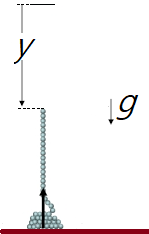
사슬(길이=$L$, 질량=$M$)이 수직으로 바닥으로 떨어진다. 다 떨어지는 순간 바닥이 받는 힘은?
1. $Mg$
2. $2Mg$
3. $3Mg$
우선 떨어지는 부분은 사슬고리 사이의 마찰 등을 무시하면 오직 중력에 의해서 자유낙하한다. 사슬이 바닥에 닿을 때 바닥이 주는 충격력에( 바닥의 수직항력) 의해서 정지하게 된다. 따라서 떨어지는 부분(관심 대상은 떨어지고 있는 부분과 충격력에 의해서 순간 정지하는 미소 질량까지 포함된 계이다. 왜냐면 바닥의 충격력 $f$가 미소 질량에 외력으로 작용하기 때문임)에 작용하는 알짜힘은 자체의 중력과 바닥이 주는 충격력$(f)$이다. 떨어지는 부분의 질량 $m(t)$는 시간에 따라 계속 변하고, 자유낙하이므로
$$y(t)=\frac{1}{2} gt^2, \quad m(t)=\lambda (L- y)= \lambda (L -\frac{1}{2} gt^2 ) ,$$
로 주어진다. 운동방정식은(아래 방향=+)
$$ \frac{dp}{dt} = \sum F_y = m g - f(t).$$
이다. 그리고$$ \frac{dp}{dt}= \frac{d(m v )}{dt} = \frac{dm}{dt} v + m \frac{ d v}{dt} = - \lambda g t^2 + m g $$
이므로 떨어지는 부분이 바닥으로부터 받는 충격력은
$$ -\lambda g^2 t^2 + mg = mg - f(t) \quad \longrightarrow \quad f(t)=\lambda g^2 t^2.$$
사슬이 완전히 바닥에 떨어지는데 걸리는 시간은 $L$ 높이에서 자유낙하하는 데 걸린 시간
$$y=L\quad \longrightarrow \quad t=\sqrt{\frac{2L}{g}},$$
이므로 다 떨어지는 순간 $f$는
$$ f(y=L) = \lambda g^2 \left(\sqrt{\frac{2L}{g}} \right)^2= 2\lambda g L = 2Mg. $$
이 순간 바닥에 작용하는 알짜힘은 $f$의 반작용과 이미 바닥에 정지한 사슬의 무게이므로
$$ F_{bot} = f(y=L) +Mg = 3Mg.$$

보다 직관적으로는 사슬의 떨어지는 끝부분이 바닥에 닿는 순간 속도가 유한한 값에서 0으로 변하므로 바닥으로부터 끊임없이 충격량을 받아야 한다. $dm$의 질량이 정지하려면 바닥이 제공해야 할 충격량 $dJ$은
$$dJ = dm (v-0) = (\lambda dy)v \quad \rightarrow \quad f = \frac{dJ}{dt} =\lambda \frac{dy}{dt} v = \lambda v^2.$$
다 내려오는 순간 사슬의 속력은 $v^2 = 2gL$ 이므로, $f= \lambda (2gL) =2Mg$.
참고 영상: https://www.youtube.com/watch?v=hoU_9DGMfzs
'Physics > 역학' 카테고리의 다른 글
| 실패가 구르는 방향은? (0) | 2016.01.20 |
|---|---|
| 누가 더 먼저 떨어지는가? (0) | 2016.01.19 |
| 누가 제일 무겁다고 느낄까? (0) | 2016.01.19 |
| 역학적 에너지는 보존되는가? (3) | 2016.01.19 |
| 움직일 수 있는 경사면을 내려오는 물체의 운동 (1) | 2016.01.19 |