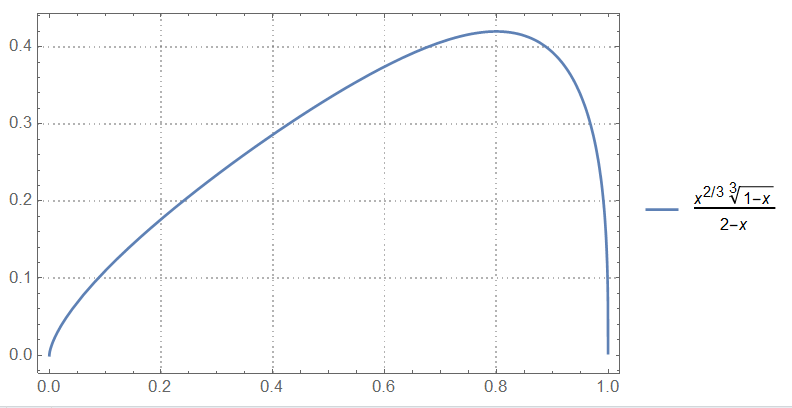
$$I = \int_0^1 \frac{x^{\alpha} (1-x)^{1-\alpha}dx}{2-x} = \frac{\pi(1+\alpha -2^\alpha)}{\sin (1-\alpha)\pi} , ~~~|\alpha | <1$$
복소평면에서 함수 $f(z)$
$$ f(z) = \frac{z^{\alpha} (z-1)^{1-\alpha}}{2-z}$$의 경로적분을 고려하자. $z=2$는 $f(z)$의 simple pole이고 residue는
$$ \text{Res}f(z=2) =- 2^{\alpha}$$
이다. 또 $ z\to\infty$일 때 전개를 하면
$$ f(z) = -1 - \frac{1+ \alpha}{z}+\cdots$$
이므로 무한대에서 residue가 존재한다.
$$ \text{Res} f(z\to\infty)= 1+\alpha$$
$z=0,2$이 branch point이므로 그림과 같이 cut line과 개뼈 경로를 선택한다. 이 경우 가능한 위상 선택은
$$ -\pi \le \text{arg}(z) \le\pi, \quad -\pi \le \text{arg}(z-1) \le \pi$$
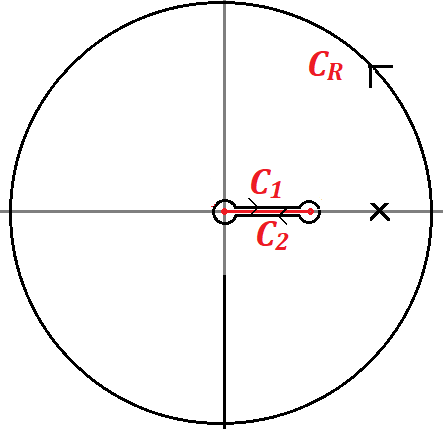
$C_\epsilon$, $C_\epsilon'$에서 경로적분이 $0$이므로 다음이 성립한다.
$$ \int_\text{dogbone} f(z) + \int_{C_R} f(z) = 2\pi i \times \text{Res}f(z=2) \\ \to \int_\text{dogbone}=2\pi i \times \left( \text{Res}f(z\to\infty) + \text{Res}f(z=2) \right)$$
그리고 $C_1$에서 $z= x e^{i0}$, $z-1=(1-x)e^{i\pi}$이므로
$$ \int_{C_1} f(z) dz = e^{i\pi (1-\alpha)} \int_0^1 \frac{x^{\alpha}(1-x)^{1-\alpha}dx}{2-x}= e^{i\pi (1-\alpha)} I $$
$C_2$에서는 $z= x^{i0}$, $z-1= (1-x) e^{-i\pi}$이므로
$$ \int_{C_2} f(z)dz = e^{-i\pi(1-\alpha)}\int_1^0 \frac{x^{\alpha}(1-x)^{1-\alpha} dx}{2-x}=- e^{-i\pi(1-\alpha)} I$$
따라서
$$ (e ^{i\pi(1-\alpha)}- e^{-i\pi(1-\alpha)}) I = 2\pi i \left( 1+\alpha - 2^\alpha\right) \qquad \to ~I = \frac{\pi}{ \sin (1-\alpha)\pi} (1+\alpha - 2^{\alpha})$$
'Mathematics' 카테고리의 다른 글
| Integration along a branch cut-023 (0) | 2024.10.06 |
|---|---|
| Integration along a branch cut-022 (0) | 2024.10.05 |
| Integration along a branch cut-020 (0) | 2024.09.28 |
| Integration along a branch cut-019 (0) | 2024.09.25 |
| Integration along a branch cut-018 (0) | 2024.09.25 |




