$$ I = \int_{-\infty}^\infty \frac{\log(1+x^2) dx}{1+x^2} = \pi\log 4$$

복소평면에서
$$f(z) = \frac{\log(1+z^2) }{1+z^2}$$
의 contour 적분을 이용해서 구하자.

$\log( 1+z^2)$의 branch point와 $f(z)$의 simple pole이 겹치기 때문에 이 적분은 $ f_1(z) = \frac{\log(z+i)}{1+z^2}$과 $f_2(z) = \frac{\log(z-i)}{ 1+z^2}$으로 나누어서 하는 것이 더 쉽지만 여기서는 분리하지 않고 하도록 하자. 우선 $\log(1+z^2)$의 branch cut과 적분경로를 그림처럼 선택하자. 그러면
$$ \left( \int_{C_\infty} + \int_{C_\epsilon} + \int_{\gamma_0} +\int_{ \gamma_1}\right) f(z) dz + I = 0$$ 이고
$$ \int_{C_\infty} f(z) dz \to 0$$
임도 쉽게 확인할 수 있다.

$$ \log (z^2+1) = \log |z^2 + 1| + i\text{arg}(z-i) + i \text{arg}(z+i)$$
이고 cutline을 시계방향으로 건널 때 $+2\pi$만큼 위상이 변하므로
\begin{align} \left( \int_{\gamma_0} + \int_{\gamma_1} \right) f(z)dz &= - \int_{\gamma_1} \frac{\log |z^2 +1| + i(\frac{\pi}{2} + 2\pi + \text{arg}(z+i))}{z^2+1} dz \\ &+ \int_{\gamma_1} \frac{ \log|z^2+1| + i (\frac{\pi}{2} + \text{arg}(z+i))}{z^2 + 1}dz \\ = -2\pi i \int_{\gamma_1} \frac{dz}{1+z^2} \end{align}
여기서 반직선 $\gamma_1$을 따른 선적분은(발산하므로 발산항을 따로 분리한다)
\begin{align} -2\pi i \int_{\gamma_1} \frac{dz}{1+z^2} &= -2\pi i \int_{i(1+\epsilon)}^{i \infty} \frac{dz}{1+z^2} = 2\pi \int_{1+\epsilon} ^ \infty \frac{dx}{1-x^2} \\ &= \pi \left. \log \frac{x+1}{x-1} \right|_{1+\epsilon}^\infty = -\pi (\log 2 - \log\epsilon) \end{align}
$\log \epsilon$ 항은 $C_\epsilon$에서의 적분결과로 상쇄시킬 수 있다. $C_\epsilon$은 $z=i + \epsilon e^{i \theta}, (\theta: \frac{\pi}{2}\to \frac{-3\pi}{2})$로 매개화를 할 수 있으므로
\begin{align} \int_{C_\epsilon} f(z) dz &= \int _{\pi /2}^{-3\pi /2} \frac{ \log (2i) + \log \epsilon + i \theta }{\epsilon e^{i \theta}\times 2i } i \epsilon e^{i \theta} d \theta \\ &= -\pi \log (2i) - \pi \log \epsilon + \left. \frac{i}{4} \theta ^2 \right|_{\pi/2}^{-3\pi/2} \\ &= -\pi\log 2 - \pi\log \epsilon \end{align}
따라서 반직선 적분에서 나온 $\log \epsilon$이 상쇄됨을 알 수 있다.
$$ I = \pi \log 4$$
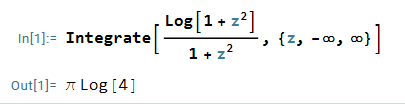
'Mathematics' 카테고리의 다른 글
| Integration along a branch cut-020 (0) | 2024.09.28 |
|---|---|
| Integration along a branch cut-019 (0) | 2024.09.25 |
| Integration along a branch cut-017 (0) | 2024.09.23 |
| Integration along a branch cut-016 (1) | 2024.09.22 |
| 물리법칙을 이용한 적분 구하기 (3) | 2024.08.30 |




