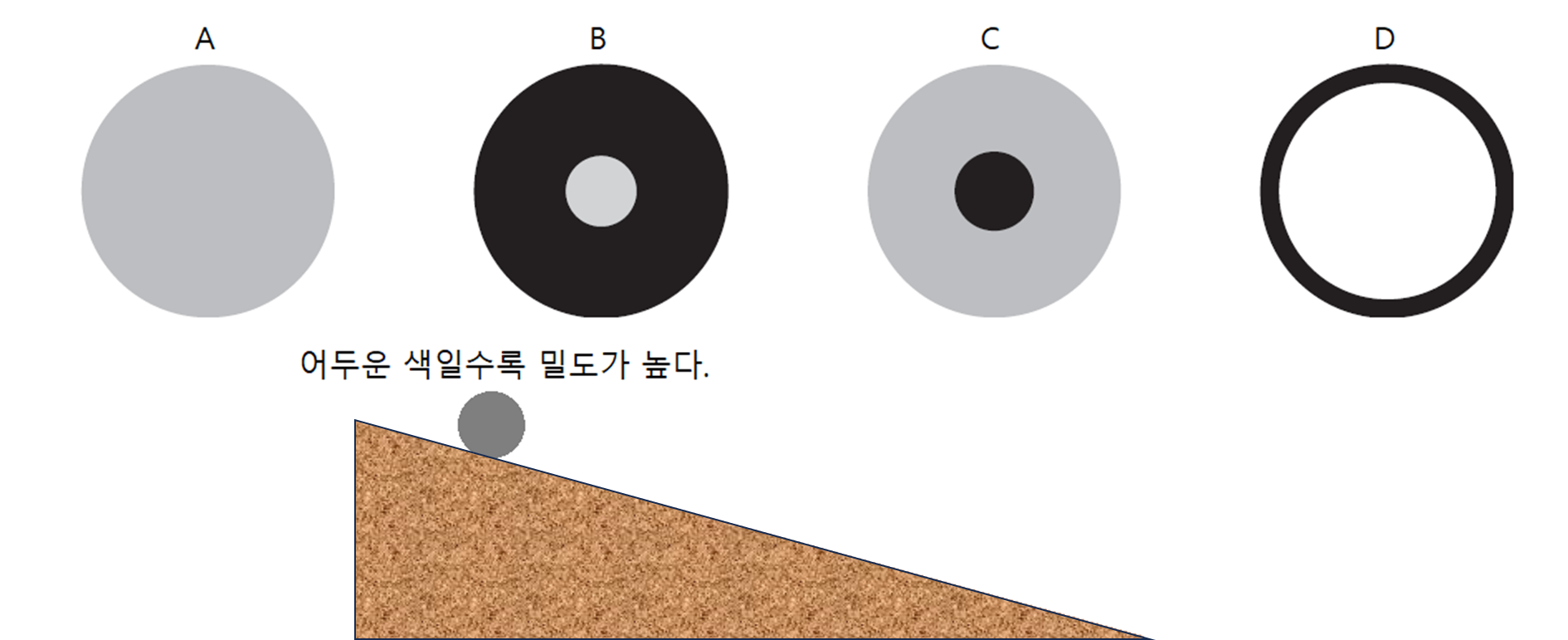
4개의 회전체가 경사면 위 같은 높이에서 출발한다. 미끄러짐이 없는 경우 바닥에 먼저 도착하는 물체는?
- A
- B
- C
- D
- 동시에
- 정보 부족
728x90
'Physics > 역학' 카테고리의 다른 글
| 공의 탄성 충돌에서 역학적 에너지 보존? (0) | 2021.01.07 |
|---|---|
| 어느 줄에 걸리는 장력이 가장 작은가? (1) | 2020.12.30 |
| 어느 물체가 더 빨리 도달하는가? (0) | 2020.12.27 |
| 얼마나 늘어날까? (0) | 2020.12.24 |
| 줄이 끊긴 직후 가속도는? (1) | 2020.12.22 |




