Geometry & Recognition

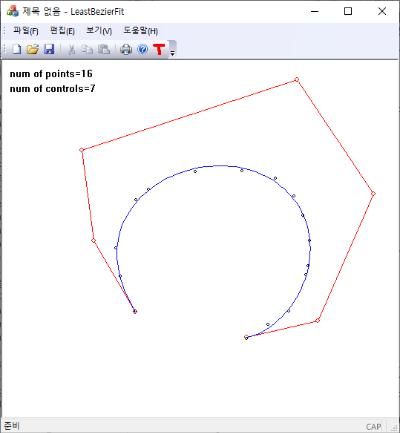
주어진 control point로 만들어지는 Bezier 곡선을 계산할 때 De Casteljas 알고리즘을 이용하여 계산한다. 이 경우 control points을 백업하는 과정이 필요하다. 여기서는 직접적으로 Bernstein 함수를 계산하여 Bezier 곡선을 구하자. 우선 control point가 ${\bf Q}_i$일 때 $n$차 Bezier 곡선을 Bernstein 다항식을 써서 표현하면

$$ {\bf B}(t) = \sum _{k=0}^n b_{k, n}(t) {\bf Q}_k \\ b_{k, n}(t) = \begin{pmatrix} n \\k \end{pmatrix} t^k (1-t)^{n-k}$$

이므로 이항계수의 계산이 요구된다. 

$$ \begin{pmatrix} n \\k \end{pmatrix} = \frac{ n!}{k! (n-k)!} $$

이항계수는 미리 계산된 lookup table을 이용하는 경우가 더 편리할 수 있다: https://kipl.tistory.com/575

// n = degree of a Bezier curve == Q.size()-1;
double Bezier(const int n, const std::vector<double>& Q, const double t) { 
    double b = 0;
    double tk = 1; 
    double onetk = pow(1-t, double(n)); 
    for (int k = 0; k <= n; k++) { 
        double blend = tk * onetk;   // bernstein polynomial; 
        // for the next stage;
        tk *= t;              
        onetk /= (1-t);     
        // multiply binomial coefficient;
        int nf = n;           // n! 계산;
        int kf = k;           // k! 계산; 
        int nkf = n-k;        // (n-k)! 계산;
        while (nf >= 1) {
            blend *= nf;      // multiply by n!
            nf--;
            if (kf > 1) {     // divide by k!
                blend /= kf; 
                kf--; 
            } 
            if (nkf > 1) {    // divide by (n-k)!
                blend /= nkf; 
                nkf--; 
            } 
        } 
        b += Q[k] * blend; 
    } 
    return b; 
}

$$ \{ {\bf C}_k \} =\text{argmin}(L) \\ L = \sum_{k=0}^{N-1} \left|  {\bf P}_k - \sum_{i=0}^n  b_{i,n} (t_k ) {\bf C} _i   \right|^2 $$

\begin{gather} t_k = d_k / d_{N-1}, \quad d_k = d_{k-1} + | {\bf P}_k -{\bf P}_{k-1}|\end{gather}

$$\text{Bernstein basis polynomial: } b_{i, n} (t)= \begin{pmatrix} n \\i \end{pmatrix} t^{i} (1-t)^{n-i} = \sum_{j=0}^n t^j  M_{ji} $$

$$ M_{ji} = \frac{n!}{(n-j)!} \frac{ (-1)^{j+i}}{ i! (j-i)!} =(-1)^{j+i}  M_{jj} \begin{pmatrix} j\\i  \end{pmatrix} \quad (j\ge i)$$

$$ \text{note: }~M_{jj} = \begin{pmatrix} n\\j \end{pmatrix},\qquad M_{ji}=0\quad (j<i)$$

// calculate binomial coefficients using Pascal's triangle
void binomialCoeffs(int n, double** C) {
    // binomial coefficients
    for (int i = 0; i <= n; i++)
        for (int j = 0; j <= i; j++)
            if (j == 0 || j == i) C[i][j] = 1;
            else                  C[i][j] = C[i - 1][j - 1] + C[i - 1][j];
}
std::vector<double> basisMatrix(int degree) {
    const int n = degree + 1;
    std::vector<double* > C(n);
    std::vector<double> Cbuff(n*n);
    for (int i = n; i-->0;) 
        C[i] = &Cbuff[i * n];
    // C[degree, k]; k=0,..,degree)
    binomialCoeffs(degree, &C[0]);
    // seting the diagonal;
    std::vector<double> M(n * n, 0); // lower triangle; 
    for (int j = 0; j <= degree; j++)
        M[j * n + j] = C[degree][j];
    // compute the remainings;
    for (int i = 0; i <= degree; i++) 
        for (int j = i + 1; j <= degree; j++)
            M[j * n + i] = ((j + i) & 1 ? -1 : 1) * C[j][i] * M[j * n + j];
    return M;
}