저울의 눈금은 어떻게 변할까?

Physics/유체역학 2016. 1. 25. 16:37

스티로폼을 줄을 이용해서 용기의 물에 완전히 잠기도록 하였다. 이 경우 스티로폼에 작용하는 부력은 스티로폼의 무게와 줄의 장력에 의해서 균형을 이룬다. 연결된 줄을 끊어서 스티로폼이 물에 떠 있는 상황이 되면 저울의 눈금은 어떻게 변할까?

1. 증가한다: 줄이 위로 당기는 힘이 사라져 그릇 무게가 그대로 저울에 작용하므로 

2. 감소한다: 스티로폼이 뜨면 물의 높이가 내려가서 바닥을 누르는 압력이 줄어들므로(압력은 높이에 비례)

3. 변함없다: 어차피 그릇+물+스티로폼의 무게는 변함없으므로

4. 정보가 부족하다.

728x90
저작자표시 비영리 변경금지

'Physics > 유체역학' 카테고리의 다른 글

유체 기둥이 잘못된 것은?  (1) 2016.01.27
무엇이 잘못 되었을까?  (0) 2016.01.26
떨어지는 물병에 뚫린 구멍에서 물이 샐 수 있나?  (0) 2016.01.24
용기 바닥에 작용하는 수압은? 저울의 눈금은?  (0) 2016.01.19
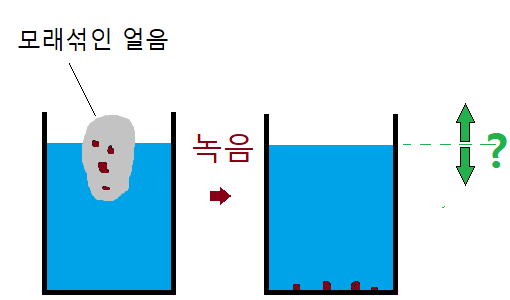
모래가 섞인 얼음이 녹을 때 수면의 높이는?  (0) 2016.01.19
Posted by helloktk
,

모래가 섞인 얼음이 녹을 때 수면의 높이는?

Physics/유체역학 2016. 1. 19. 12:13

모래가 섞인 얼음을 물이 담긴 컵에 넣었더니 물에 뜬다. 얼음이 다 녹으면 수면의 높이는 어떻게 될까?

1. 올라간다.

2. 변함없다.

3. 내려간다.

4. 모래의 양에 따라 다르다.

 

더보기

얼음이 뜨는 이유는 부력 때문이다. 부력의 크기는 얼음의 무게와 같고, 또 얼음의 잠긴 부분이 밀어낸 물의 무게와 같다. 불순물이 없는 얼음의 경우 다 녹으면 물이 되고 이 물의 무게(=얼음의 무게)는 잠긴 부분이 밀어낸 물의 무게와 같으므로 수면은 변화가 없다. (얼음이 녹아 생긴 물의 양은 원래 잠긴 부분을 채울 만큼이다)

 

모래가 섞인 얼음에서 얼음 부피를 $V_{ice}$, 모래 전체의 부피를 $V_{sand}$라면

$$\text {부력=모래 얼음 부피} \rightarrow \rho_w g V_\text {잠김}=\rho_{ice} gV_{ice}+\rho_{sand} g V_{sand}\\ \therefore V_\text{잠김}= \frac{\rho_{ice}}{\rho_{w}} V_{ice} + \frac{\rho_{sand}}{\rho_{w}} V_{sand}$$

여기서, $\frac {\rho_{ice}}{\rho_{w}} V_{ice}$는 순수한 얼음이 밀어낸 물의 부피로, 앞에서 설명한 대로 수면의 높이를 변화시키지 않는다. 그러나 $\frac {\rho_{sand}}{\rho_{w}} V_{sand}(> V_{sand})$는 모래(전체)를 띄우기 위해서 밀려난 물 부피이다. 얼음이 녹아 모래가 가라앉으면 $V_{sand}$만큼의 물이 밀려나므로 수면은 내려가게 된다:

$$V_\text{잠김} > \frac{\rho_{ice}}{\rho_{w}} V_{ice} + V_{sand}$$

 

이는 배에 실린 돌을 물에 던지면 수면이 내려가는 이치와 같다.

 

돌을 띄우는 부력을 만들기 위해 밀어낸 물의 양은 돌이 가라앉았을 때 밀어낸 물의 양보다 많다.

 

 

Q1. 기포가 섞인 얼음이 녹으면 수면은 어떻게 될까?(기포의 무게는 무시할 수 있다).

Q2. 배에 실린 가벼운 스티로폼을 물에 던지면 수면은 어떻게 될까?

728x90
저작자표시 비영리 변경금지

'Physics > 유체역학' 카테고리의 다른 글

유체 기둥이 잘못된 것은?  (1) 2016.01.27
무엇이 잘못 되었을까?  (0) 2016.01.26
저울의 눈금은 어떻게 변할까?  (1) 2016.01.25
떨어지는 물병에 뚫린 구멍에서 물이 샐 수 있나?  (0) 2016.01.24
용기 바닥에 작용하는 수압은? 저울의 눈금은?  (0) 2016.01.19
Posted by helloktk
,

티스토리툴바