comb 함수: 일정한 간격($T$)으로 주어진 message를 샘플링하는 함수.
$$\text{comb}_T(t) := \sum_{n=-\infty}^{\infty} \delta (t- nT)$$
주기가 $T$인 함수다:
$$ \text{comb}_T(t) = \text{comb}_T(t+T)$$
따라서 Fouries series 전개가 가능하다.
$$\text{comb}_T(t) = \sum_{n=-\infty}^{ \infty} c_n e^{i 2\pi n t /T}$$
계수 $c_n$은?
\begin{align} c_n :=&\frac{1}{T} \int_{-T/2}^{T/2} \text{comb}_T(t) e^{-i 2\pi n t /T}dt \\ =& \frac{1}{T}\int_{-T/2}^{T/2} \delta (t) e^{ -i 2\pi n t/T} dt \\ =&\frac{1}{T} e^{-i 2\pi n (0) /T } = \frac{1}{T}.\end{align}
따라서, $\text{comb}_T(t)$의 Fourier series 전개는
$$\text{comb}_T(t) = \frac{1}{T} \sum_{n = -\infty}^{\infty} e^{i2\pi n t/T}.$$
frequency domain에서 delta 함수의 역 Fourier transform은 정의에 의해서
$$ {\cal F}^{-1} [\delta (f-f_0)] = \int \delta (f-f_0) e^{i 2\pi t f }df = e^{i 2\pi t f_0}$$
그럼 $\text{comb}_T(t)$의 Fourier transform은 어떻게 표현되는가?
\begin{align} {\cal F}[\text{comb}_T(t)]=& \frac{1}{T} \sum {\cal F}[ e^{i2\pi n t/T}] \\ =& \frac{1}{T} \sum {\cal F}[ {\cal F}^{-1} [ \delta (f - n/T)]] \\ =& \frac{1}{T} \sum_{n = -\infty}^{\infty} \delta(f - n/T).\end{align} $\text{comb}$ 함수의 Fourier 변환은 frequency domain에서 $\text{comb}$ 함수이고 (up to constant factor), time domain에서 주기가 $T$일 때 frequency domain에서는 $ 1/T$의 주기를 가진다.
주어진 message $m(t)$에서 일정한 간격 $T$로 샘플링된 message $m_s(t)$는 $\text{comb}$ 함수를 이용하면
$$m_s (t) : = m(t) \text{comb}_T(t) = \sum m(nT) \delta (t- nT)$$
로 표현된다.
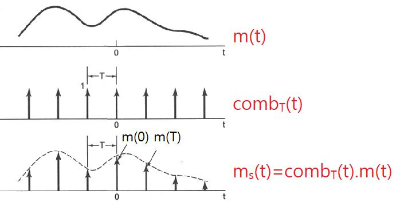
양변에 Fourier transform을 적용하면,
\begin{align} M_s(f) = {\cal F} [m_s ] =& {\cal F}[m(t) \text{comb}_T(t)]= {\cal F}[m] * {\cal F}[\text{comb}_T] \\ =& \frac{1}{T} \sum \int \delta(f' - n /T) M(f- f') df' \\ =& \frac{1}{T} \sum_{n=- \infty}^{\infty} M(f - n/T) . \end{align}
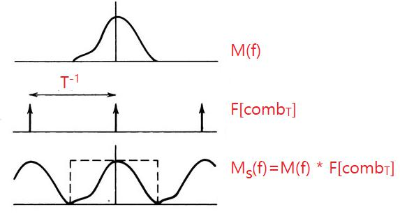
따라서 message의 spectrum이 band-limited이고, $\text{band-width} \le \frac{1}{2} f_s = \frac{1}{2T}$인 조건을 만족하면 샘플링된 데이터를 이용해서 원 신호를 복원할 수 있다.

이 경우에 low-pass filter
$$ H(f/f_s) := T \cdot \text{rect}(f/f_s)=\left\{ \begin{array}{ll} T ,& |f/f_s| < 1/2 \\ 0 , & |f/f_s| >1/2,\end{array}\right. $$
을 sampled massage의 Fourier transform에 곱해주면, 원 message의 Fourier transform을 얻는다:
$$ M(f) = H(f) M_s(f).$$
그런데 $M_s(f)$는 frequency domain에서 주기가 $f_s = 1/T$인 주기함수이므로 Fourier series로 표현할 수 있다:($\text{comb}_T$ 함수와 같은 방식으로 하면 계수를 쉽게 찾을 수 있다: Poisson summation formula)
$$M_s(f) = \frac{1}{T}\sum M(f- n f_s ) = \sum_{-\infty}^\infty m(nT) e^{-i 2\pi nf T}$$
따라서,
\begin{align} M(f) = & H(f/f_s) M_s(f) \\ =& H(f/f_s) \sum m(nT) e^{-i 2\pi nfT} \\ =& \sum m(nT) \Big(\text{rect}(f/f_s )T e^{-i 2\pi nTf} \Big) \\=& \sum m(nT) {\cal F} \left[ \text{sinc} \left( \pi \frac{t-nT}{T} \right) \right]\end{align}
이므로 양변에 역 Fourier transform을 하면 sampled 된 message $\{m(nT)|n\in Z\}$를 이용해서 원 message를 복원할 수 있는 식을 얻을 수 있다(Whittaker-Shannon interpolation):
$$m(t) = \sum_{n=-\infty}^{\infty} m(nT) \,\, \text{sinc}\left( \pi \frac{t-nT}{T} \right) .$$
'Image Recognition > Fundamental' 카테고리의 다른 글
| Orientation 추정 (0) | 2021.11.30 |
|---|---|
| Poisson Image Editing (0) | 2021.08.03 |
| Lanczos Resampling (0) | 2021.05.08 |
| Interpolation Kernels (0) | 2021.05.05 |
| Fowler Angle (0) | 2021.04.05 |




