Geometry & Recognition

공기 저항이 속력에 비례하는 경우는 물체의 궤적은 closed form이 있다. 그러나 저항력이 속력의 제곱에 비례하게 주어지는 경우는 수치적으로 해결해야 한다. 움직이는 방향의 단면적이 $A=\frac{1}{4}\pi D^2$인 물체가 밀도가 $\rho$인 공기 속에서 $\vec{v}$의 속도로 움직일 때 저항력은 

$$ {\vec F}_D = \frac{1}{4} \rho A v \vec{v}=\frac{1}{16}\pi \rho D^2 v\vec{v}=c v \vec{v}$$

로 표현할 수 있다. 따라서 물체의 운동방정식은

$$ m \ddot{\vec r} = m\vec{g}- c v \vec{v},$$

또는 성분으로 쓰면

$$ m \ddot{x} = - c \sqrt{ \dot{x}^2 + \dot{y}^2} \dot{x}, $$

$$m \ddot{y} = -mg - c \sqrt{\dot{x}^2+ \dot{y}^2} \dot{y}$$

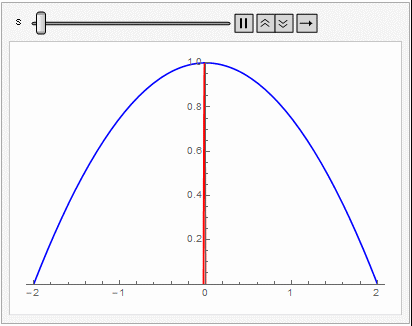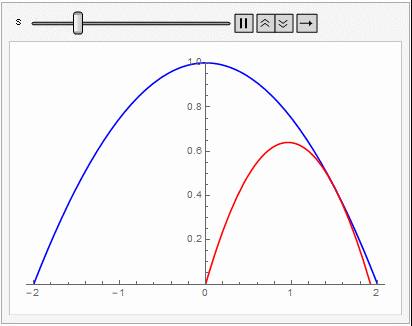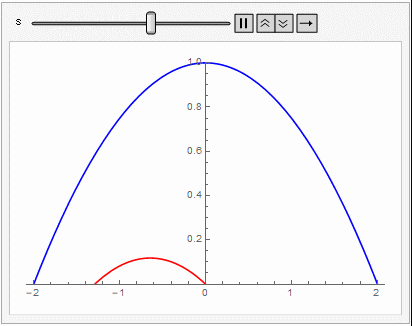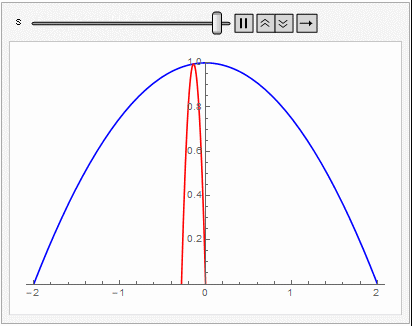
로 주어진다. 아래의 mathematica 코드는 구체적인 수치(SI-단위 기준, 발사각 $\theta_0$, 발사속력 $v_0$)를 대입해서 공기저항이 있을 때와 없을 때 물체의 궤적을 보여준다.

공기 저항이 있을 때 (2)

한 지점에서 일정한 속력으로 마구 쏘아대는 대공포가 있을 때 포탄이 도달할 수 없는 영역은 어떻게 찾을 수 있을까? 유한한 발사속력 때문에 도달할 수 있는 영역에는 분명히 한계가 있다.

공기 저항을 무시할 때 포탄이 그리는 궤적은 포물선이 된다. 따라서 포탄에 맞지 않으려면 포탄이 그리는 가능한 모든 포물선에 접하는 곡선 밖에 있어야 할 것이다. 발사 각도가 $ \theta$일 때, $v_0$ 속력으로 발사한 포탄이 그리는 포물선은

$$ y= \tan \theta x - \frac{1}{4H \cos ^2 \theta} x^2.$$

로 표시된다. 여기서 $H=v_0^2/2g$는 포탄이 도달할 수 있는 최고 높이다. 

발사 평면의 한 점 $(x_0, y_0)$에 포탄이 도달하기 위해서는 

$$ y_0 = \tan \theta x_0 + \frac{1}{4H \cos ^2 \theta} x_0^2$$

을 만족시키는 발사각 $\theta$가 있어야 한다. $1/\cos^2 \theta = 1+ \tan^2 \theta$이므로 위 식은 $\tan \theta$에 대한 이차식이므로 일반적으로 발사각이 2개가 있다. 만약 $(x_0, y_0)$가 포탄에 맞는 경계영역에 있다면 근이 하나가 있을 것이고, 포탄이 도달할 수 없는 영역에 있다면 근이 존재할 수 없다. 따라서 포탄이 도달할 수 있는 영역의 경계는 이 $\tan \theta$에 대한 이차방정식이 중근을 가질 때 $(x_0, y_0)$의 자취로 주어진다.

위 식을 정리하면 

$$ \frac{x_0^2}{4H}   \tan ^2  \theta + x_0 \tan \theta + \frac{x_0^2 }{4H} - y_0 = 0$$

이므로 판별식이 0일 조건은 

$$ x_0^2 - 4 \frac{x_0^2}{4H}  \Big(\frac{x_0^2}{4H} - y_0\Big) = 0 \quad \Rightarrow\quad y_0 = H - \frac{1 }{4H} x_0^2$$

로 쓰인다. 따라서 대공포로 부터 안전한 영역의 경계는 다음에 주어지는 포물선 바깥 영역이다.

$$\frac{ y}{H} =   1-  \frac{x^2}{R^2}  $$

여기서 $R=2H$는 $v_0$로 발사했을 때 최대 수평 도달거리를 나타낸다. 3차원 공간에서는 안전영역의 경계는 이 포물선을 주축에 대해서 회전시킨 포물면이 될 것이다.

중력이 일정하지 않고 $1/r^2$으로 변할 때 지상에 다시 떨어지는 물체의 경로는 지구의 중심을 한 초점으로 하는 타원의 일부분이 된다. 이 경우 물체 궤도의 envelope은 어떻게 주어질까?

$(1,1)$에서 $(0,0)$까지를 연결하는 일차 곡선 ($y=x$), 이차 곡선 ($y=x^2$), 6차 곡선 ($y=x^6$), 사분원 ($y=1-\sqrt{1-x^2}$) 그리고 cycloid ($x=1-R(\theta-\sin\theta), y=1-R(1-\cos\theta)$) 위를 움직이는 물체의 운동을 mathematica를 사용해서 animation으로 표현하는 방법을 알아보자. 중력가속도는 $g=1$로 놓는다. 적절한 generalized coordinate를 선택해서 Euler-Lagrange equation을 이용하면 운동방정식을 쉽게 구할 수 있다.

(A)  곡선이 $y=f(x)$의 형태로 주어지는 경우 운동방정식은

$$\big[ 1+ (f')^2 \big] \ddot{x} + f' f''  \dot{x} ^2 + f'= 0 .$$

직선경로를 제외하면 운동방정식은 비선형이므로 mathematica의 $\tt NDSolve[]$을 이용해서 수치적으로 푼다.

(B) 원의 경우는 $x$ 좌표보다는 각변수를 이용하면 apparent singularity를 피할 수 있다. 이 경우 운동방정식은

$$ \ddot{\theta} = -\sin \theta,$$

로 주어진다. 

(C) cycloid는 곡선을 따라 움직이는 시간

$$t =\int \frac{ds}{v} = \int  \sqrt{\frac{1 + (dx/dy)^2}{2g(1-y)}}dy$$

을 최소로 만들어주는 곡선이다. cycloid는 다음과 같이 $R$ 변수와 각도 변수 $\theta$로 표현할 수 있다.

$$ 1-x=R(\theta-\sin \theta),~~y-1= -R(1-\cos \theta)$$

이 곡선이 $(0,0)$을 지나야 하는 조건에서 $R$과 그 때의 $\theta$ 값을 구할 수 있다. 먼저 $\theta$을 소거하면,

$$ R \cos \Big( \frac{1+\sqrt{2R-1}}{R} \Big) + 1 = R $$

을 얻고, 이 식의 근을 구하면 $R$ 값이 정해진다. 또한, $$1=R(\theta- \sin \theta)$$을 풀어서 $(0,0)$에 도달할 때 $\theta=\theta_0$ 값을 얻을 수 있다. 그리고 시간과 $\theta$ 변수의 관계는 위의 표현을 적분에 대입하면 

$$t = \sqrt{ \frac{R}{g} }  \theta $$

로 주어짐을 알 수 있다. 이는 사이클로이드가 일정하게 굴러가는 바퀴의 한 점이 그리는 자취이기 때문이다.

아래는 5가지 경우의 곡선 각각에서 운동을 보여주는 mathematica 코드다. 곡선의 모양에 따라 바닥에 도착하는 시간이 다름을 알 수 있다. 출발 높이가 $H$일 때 걸리는 시간은 $\sqrt{H/g}$ 단위로 

직선: $t_1=\int_0^1{ \frac{dy}{\sqrt{1-y}}} = 2$

2차 곡선: $t_2=\int_0^1\sqrt{ \frac{1+4y}{8y(1-y)}}dy= 1.86336$

6차 곡선: $t_6=\int_0^1 \sqrt{\frac{1+36y^{5/3}}{72y^{5/3}(1-y)}}dy=1.90954$

4분원: $t_c=\int_0^{\pi/2} \frac{d \theta}{\sqrt{2\sin \theta }}=1.85407$

cycloid: $t_0= \sqrt{R}\theta_0 = 1.82568$

(* coordinate 벡터의 크기로 차원 결정한다: n=Length[vars]; *)

InverseMetric[g_] := Simplify[Inverse[g]]

ChristoffelSymbol[g_, vars_] := 
 Block[{n, ig, res}, n = Length[vars]; ig = InverseMetric[g];
  res = Table[(1/2) * Sum[ig[[i, s]] *

         (-D[g[[j, k]], vars[[s]]] + D[g[[j, s]], vars[[k]]] + D[g[[s, k]], vars[[j]]]), {s, 1, n}],

         {i, 1, n} , {j, 1, n} , {k, 1, n}];
  Simplify[res]]

RiemannTensor[g_, vars_] := 
 Block[{n, Chr, res}, n = Length[vars]; 
  Chr = ChristoffelSymbol[g, vars];
  res = Table[

    D[Chr[[i, k, m]], vars[[l]]] - D[Chr[[i, k, l]], vars[[m]]] + 
    Sum[Chr[[i, s, l]]*Chr[[s, k, m]], {s, 1, n}] - 
    Sum[Chr[[i, s, m]]*Chr[[s, k, l]], {s, 1, n}], 

     {i, 1, n} , {k, 1, n} , {l, 1, n} , {m, 1, n}];
  Simplify[res]]

RicciTensor[g_, vars_] := 
 Block[{n, Rie, res}, n = Length[vars]; Rie = RiemannTensor[g, vars];
  res = Table[
    Sum[Rie[[s, i, s, j]], {s, 1, n}], 

    {i, 1, n} , {j, 1, n}];
  Simplify[res]]

RicciScalar[g_, vars_] := 
 Block[{n, Ricci, ig, res}, n = Length[vars]; 
  Ricc = RicciTensor[g, vars]; ig = InverseMetric[g];
  res = Sum[ig[[s, i]] Ricc[[s, i]], {s, 1, n} , {i, 1, n}];
  Simplify[res]]

예제: 구대칭 metric

$$ds^2 = -e^{ 2\nu(r)} dt^2 + e^{2\lambda(r)} dr^2 + r^2 d\theta^2 + r^2 \sin^2 \theta d\varphi^2$$

vars = {t, r, \[Theta], \[Phi]};

g = {{-Exp[2 \[Nu][r]], 0, 0, 0}, {0, Exp[2 \[Lambda][r]], 0, 0}, {0, 
    0, r^2, 0}, {0, 0, 0, r^2 Sin[\[Theta]]^2}};

RicciTensor[g, vars]

결과:

Mathematica에서 shooting method를 이용해서 비선형 미분방정식의 해를 구하자. 

\begin{align}f' &= \frac{1}{x} (1-a) f \\ a'&=- \frac{x}{2} f^2 (f^2-1) \end{align}

경계조건은 $f(0)=0$, $f(\infty)\to 0$, $a(0)=0$을 만족시켜야 한다. $x$가 증가하면 $f(x)$는 빠르게 $1$로 수렴하므로 오른쪽 경계조건은 $f(15)\to1$로 잡아도 충분하다. $x=0$에서의 apparent singularity를 Mathematica가 처리할 수 있도록 방정식을 변형시켜주어야 한다.