Parabola of Safety

safetyparabola.nb

0.01MB

한 지점에서 일정한 속력으로 마구 쏘아대는 대공포가 있을 때 포탄이 도달할 수 없는 영역은 어떻게 찾을 수 있을까? 유한한 발사속력 때문에 도달할 수 있는 영역에는 분명히 한계가 있다.

 

공기 저항을 무시할 때 포탄이 그리는 궤적은 포물선이 된다. 따라서 포탄에 맞지 않으려면 포탄이 그리는 가능한 모든 포물선에 접하는 곡선 밖에 있어야 할 것이다. 발사 각도가 $ \theta$일 때, $v_0$ 속력으로 발사한 포탄이 그리는 포물선은

$$ y= \tan \theta x - \frac{1}{4H \cos ^2 \theta} x^2.$$

로 표시된다. 여기서 $H=v_0^2/2g$는 포탄이 도달할 수 있는 최고 높이다. 

 

발사 평면의 한 점 $(x_0, y_0)$에 포탄이 도달하기 위해서는 

$$ y_0 = \tan \theta x_0 + \frac{1}{4H \cos ^2 \theta} x_0^2$$

을 만족시키는 발사각 $\theta$가 있어야 한다. $1/\cos^2 \theta = 1+ \tan^2 \theta$이므로 위 식은 $\tan \theta$에 대한 이차식이므로 일반적으로 발사각이 2개가 있다. 만약 $(x_0, y_0)$가 포탄에 맞는 경계영역에 있다면 근이 하나가 있을 것이고, 포탄이 도달할 수 없는 영역에 있다면 근이 존재할 수 없다. 따라서 포탄이 도달할 수 있는 영역의 경계는 이 $\tan \theta$에 대한 이차방정식이 중근을 가질 때 $(x_0, y_0)$의 자취로 주어진다.

 

위 식을 정리하면 

$$ \frac{x_0^2}{4H}   \tan ^2  \theta + x_0 \tan \theta + \frac{x_0^2 }{4H} - y_0 = 0$$

이므로 판별식이 0일 조건은 

$$ x_0^2 - 4 \frac{x_0^2}{4H}  \Big(\frac{x_0^2}{4H} - y_0\Big) = 0 \quad \Rightarrow\quad y_0 = H - \frac{1 }{4H} x_0^2$$

로 쓰인다. 따라서 대공포로 부터 안전한 영역의 경계는 다음에 주어지는 포물선 바깥 영역이다.

$$\frac{ y}{H} =   1-  \frac{x^2}{R^2}  $$

여기서 $R=2H$는 $v_0$로 발사했을 때 최대 수평 도달거리를 나타낸다. 3차원 공간에서는 안전영역의 경계는 이 포물선을 주축에 대해서 회전시킨 포물면이 될 것이다.

 

 

 

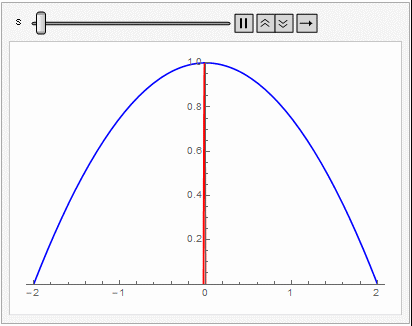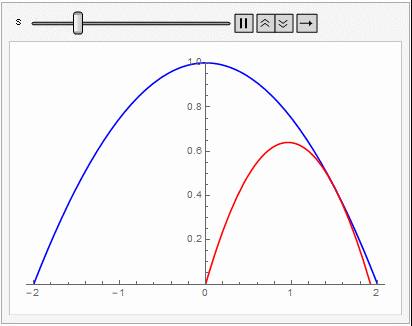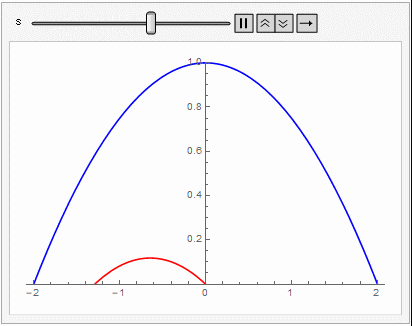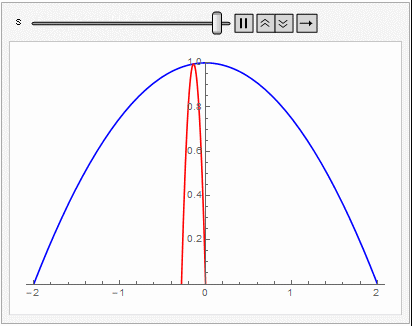
중력이 일정하지 않고 $1/r^2$으로 변할 때 지상에 다시 떨어지는 물체의 경로는 지구의 중심을 한 초점으로 하는 타원의 일부분이 된다. 이 경우 물체 궤도의 envelope은 어떻게 주어질까?