#define PIX_SORT(a,b) { if ((a) > (b)) PIX_SWAP((a), (b));}
#define PIX_SWAP(a,b) { BYTE tmp = (a); (a) = (b); (b) = tmp;}
BYTE opt_med9(BYTE p[9]) {
PIX_SORT(p[1], p[2]); PIX_SORT(p[4], p[5]); PIX_SORT(p[7], p[8]);
PIX_SORT(p[0], p[1]); PIX_SORT(p[3], p[4]); PIX_SORT(p[6], p[7]);
PIX_SORT(p[1], p[2]); PIX_SORT(p[4], p[5]); PIX_SORT(p[7], p[8]);
PIX_SORT(p[0], p[3]); PIX_SORT(p[5], p[8]); PIX_SORT(p[4], p[7]);
PIX_SORT(p[3], p[6]); PIX_SORT(p[1], p[4]); PIX_SORT(p[2], p[5]);
PIX_SORT(p[4], p[7]); PIX_SORT(p[4], p[2]); PIX_SORT(p[6], p[4]);
PIX_SORT(p[4], p[2]); return(p[4]);
}
double ImageSharpness(BYTE *img, int w, int h) {
const int npixs = w * h;
const int xend = w - 1, yend = h - 1;
const int nn[] = {-w - 1, -w, -w + 1, -1, 0, 1, w - 1, w , w + 1};
const int sobelX[] = {-1, 0, 1, -2, 0, 2, -1, 0, 1};
const int sobelY[] = {-1, -2, -1, 0, 0, 0, 1, 2, 1};
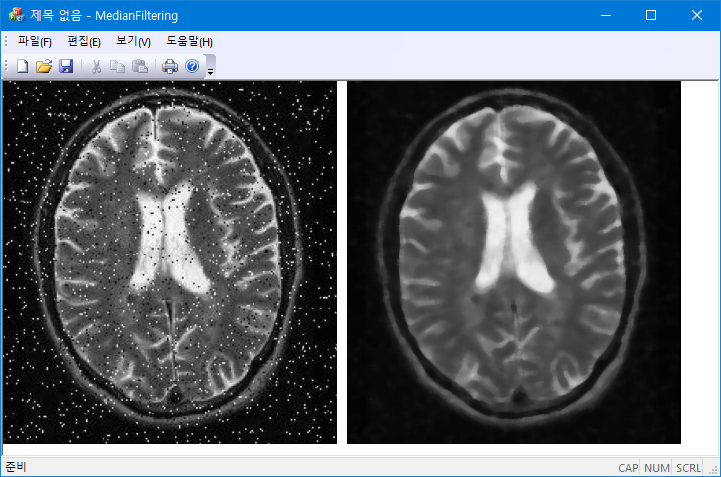
//median filter;
BYTE arr[9];
std::vector<BYTE> medimg(npixs, 0);
for (int y = 1, pos = y * w; y < yend; y++) {
pos++;
for (int x = 1; x < xend; x++, pos++) {
for (int k = 0; k < 9; k++) arr[k] = img[pos + nn[k]];
medimg[pos] = opt_med9(arr);
}
pos++;
}
// Tenenbaum gradient;
double sharpness = 0;
for (int y = 1, pos = y * w; y < yend; y++) {
pos++;
for (int x = 1; x < xend; x++, pos++) {
double gx = 0, gy = 0;
for (int k = 0; k < 9; k++) {
int v = medimg[pos + nn[k]];
gx += sobelX[k] * v;
gy += sobelY[k] * v;
}
sharpness += gx * gx + gy * gy;
}
pos++;
}
return sharpness;
}