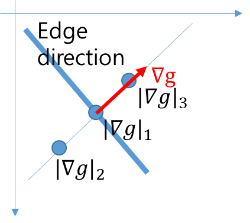
Canny 알고리즘은 영상에서 edge을 찾을 수 있게 설계된 알고리즘으로 여러 단계의 영상 처리 과정으로 구성되어 있다. 일반적으로 edge 검출기는 노이즈에 매우 민감하기 때문에 low pass filter인 Gaussian filter를 적용하여 영상의 노이즈를 제거한다. edge에 해당하는 위치에서는 edge에 수직인 방향으로 gray 값의 변동이 크다는 사실을 이용해서 edge를 찾을 수 있다. 이를 위해서 영상의 gradient field $\nabla g=(g_x, g_y)~$를 구하고, 이를 이용해서 gradient의 크기$\left( |\nabla g|=\sqrt{g_x^2 + g_y^2}\right)$와 방향 정보$\left(\theta = \tan^{-1}(g_y/g_x)\right)$를 얻는다. 대부분의 경우 edge 근방에서 gradient의 크기는 연속적으로 변하므로 edge가 두꺼운 형태가 된다. edge를 한 픽셀 두께로 줄이기 위해서는 gradient 크기의 극대점들을 찾는 추가적인 과정을 거쳐야 한다. 이 추가 처리를 non-maximal suppression이라 하는데, 이는 극대점에서 gradient 방향 또는 그 반대 방향으로 움직이는 경우 gradient 크기가 감소한다는 점을 이용한다. 아래 그림에서 1번 지점이 edge 위에 있으면 gradient 방향(edge 방향에 수직임)의 앞/뒤 지점인 2와 3에서 크기보다 커야 한다.
$$ \text{edge 조건}:~~|\nabla g|_1 > |\nabla g|_2 ~\text{and}~ |\nabla g|_1 > |\nabla g|_3$$
보통 gradient field의 방향을 수평(0, 180도), 수직(90도, 270도), 45도(225도), 135도(325도)로 나누고, 해당 방향의 인접 픽셀에서 gradient 크기를 비교하여 극대점을 판별한다. 주어진 픽셀의 8 방향 근방에서의 gradient 세기는 각각 nn, nw, ww, sw, ss, se, ee, ne로 정의했다. 예를 들면 gradient field의 방향이 거의 수평인 경우(방향이 -22.5~22.5, -180~-157.5, 157.5~180 범위에 들어가는 경우다. 이 경우 edge 방향은 거의 수직) 극대가 되려면 수평 방향의 최근방에서 크기 ee나 ww 보다 더 커야 한다.

void NonmaxSuppress(int radius, int width, int height,
std::vector<double> &gradx, std::vector<double> &grady,
std::vector<int> &edgemap) {
const double rad2deg = 45.0 / atan(1.0);
std::vector<double> mag(width * height, 0);
std::vector<double> dir(width * height, 0);
int startx = radius, endx = width - radius;
int starty = width * radius, endy = width * (height - radius);
for (int x = startx; x < endx; x++)
for (int y = starty; y < endy; y += width) {
int pos = x + y;
double gx = gradx[pos, gy = grady[pos];
mag[pos] = hypot(gx, gy);
dir[pos] = rad2deg * atan2(gy, gx);
}
for (int x = startx; x < endx; x++) { // non-maximal supression
for (int y = starty; y < endy; y += width) {
int pos = x + y;
double gmag = mag[pos];
double ang = dir[pos];
double ww = mag[pos-1];
double ee = mag[pos+1];
double nn = mag[pos-width];
double ss = mag[pos+width];
double ne = mag[pos-width+1];
double se = mag[pos+width+1];
double sw = mag[pos+width-1];
double nw = mag[pos-width-1];
bool bedge = false;
if ((0 <= ang && ang < 22.5) || (157 <= ang && ang <= 180)
|| (-22.5 <= ang && ang < 0) || ( -180 <= ang < -157.5))
bedge = (gmag >= ee) && (gmag >= ww); // 수평;
else if ((22.5 <= ang && ang < 67.5) || (-157.5 <= ang && ang > -112.5))
bedge = (gmag >= se) && (gmag >= nw); // 45도
else if ((67.5 <= ang && ang < 112.5) || (-112.5 <= ang && ang > -67.5))
bedge = (gmag >= nn) && (gmag >= ss); // 수직
else
bedge = (gmag >= sw) && (gmag >= ne); // 135도
edgemap[pos] = bedge ? int(MAG_SCALE * gmag): 0;
}
}
}gradient field의 방향 정보를 이용한 non-maximal suppression은 atan() 함수의 호출로 인해서 연산 비용이 많이 든다. 이를 해소하기 위해서 gradient 방향을 양자화하지 말고 직접 gradient 방향으로 한 픽셀 근방에서 gradient의 크기를 주변 8개 픽셀에서의 gradient 값(nn, nw, ww, sw, ss, se, ee, nw)을 이용해서 구하는 방법을 사용하자. 이 방법을 사용하면 atan()를 호출할 필요가 없어진다. 예를 들면 gradient의 방향이 0에서 45도 사이에 있다고 하자. 그러면 A 점이 극대가 되려면 A에서 gradient 방향의 연장선 상에 있는 한 픽셀 정도 떨어진 지점 B와 C에서 gradient 크기보다 더 커야 한다. B와 C에서 gradient 크기는 주변 8 방향 중에서 가장 가까이 있는 픽셀에서의 크기 ee와 se를 선형보간을 사용해서 얻을 수 있다.

\begin{align} \tt |\nabla g|_B &\approx \tt se* \tan \theta + ee* (1-\tan \theta)~~~(\text{linear interpolation}) \\ &= \tt se*\frac{gy}{gx} + ee* \left( 1-\frac{gy}{gx} \right) \\ \tt |\nabla g|_C &\approx \tt nw* \tan \theta + ww* (1-\tan \theta) \\ &= \tt nw*\frac{gy}{gx} + ww* \left( 1-\frac{gy}{gx} \right) \end{align}
극대점 판별을 다음과 같이 쓰면 나눗셈 연산도 피할 수 있다.
$$ \tt |\nabla g|_A \ge |\nabla g|_B ~~\Leftrightarrow~~ gx * |\nabla g|_A \ge se* gy + ee*(gx - gy) $$
$$ \tt |\nabla g|_A \ge |\nabla g|_C ~~\Leftrightarrow~~ gx * |\nabla g|_A \ge nw* gy + ww*(gx - gy) $$
void NonmaxSuppress(int radius, int width, int height,
std::vector<double> &gradx, std::vector<double> &grady,
std::vector<int> &edgemap) {
std::vector<double> mag(width * height, 0);
int startx = radius, endx = width - radius;
int starty = width * radius, endy = width * (height - radius);
for (int x = starx; x < endx; x++)
for (int y = 0; y < endy; y += width) {
int pos = x + y;
mag[pos] = hypot(gradx[pos], grady[pos]);
}
for (int x = startx; x < endx; x++) { // non-maximal supression
for (int y = starty; y < endy; y += width) {
int pos = x + y;
double gx = gradx[pos];
double gy = grady[pos];
double gmag = mag[pos];
double ww = mag[pos-1];
double ee = mag[pos+1];
double nn = mag[pos-width];
double ss = mag[pos+width];
double ne = mag[pos-width+1];
double se = mag[pos+width+1];
double sw = mag[pos+width-1];
double nw = mag[pos-width-1];
bool bedge = false;
if (gx * gy > = 0) {//1,3 분면
if (abs(gx) >= abs(gy)) {//0~45,180~225;
double tmp = abs(gx*gmag);
bedge = (tmp >= abs(gy*se + (gx-gy)*ee)) && (tmp > abs(gy*nw + (gx-gy)*ww));
} else {//45~90,225~270;
double tmp = abs(gy*gmag);
bedge = (tmp >= abs(gx*se + (gy-gx)*ss)) && (tmp > abs(gx*nw + (gy-gx)*nn));
}
} else {//2,4 분면
if (abs(gx) >= abs(gy)) {//135~180, 315~360;
double tmp = abs(gx*gmag);
bedge = (tmp >= abs(gy*ne - (gx+gy)*ee)) && (tmp > abs(gy*sw - (gx+gy)*ww));
} else {//90~135, 270~315;
double tmp = abs(gy*gmag);
bedge = (tmp >= abs(gx*ne - (gy+gx)*nn)) && (tmp > abs(gx*sw - (gy+gx)*ss));
}
}
edgemap[pos] = bedge ? int(MAG_SCALE * gmag): 0;
}
}
}

'Image Recognition > Fundamental' 카테고리의 다른 글
| 파라미터 공간에서 본 최소자승 Fitting (0) | 2023.05.21 |
|---|---|
| 영상에 Impulse Noise 넣기 (2) | 2023.02.09 |
| Statistical Region Merging (0) | 2022.06.11 |
| Moment-preserving Thresholding (0) | 2022.05.29 |
| Minimum Cross Entropy Thresholding (0) | 2022.05.29 |




