평균이 $\lambda$인 Poisson 분포를 가지는 random number를 만드는 레시피는 [0,1]에서 추출된 균일한 random number 수열이 $u_1, u_2, u_3,...$로 주어질 때, $u_1 u_2 u_3....u_{k+1}\le e^{-\lambda}$을 처음 만족하는 $k$를 찾으면 됨이 Knuth에 의해서 알려졌다.
int PoissonValue(double lambda) { // lambda = mean value
double L = exp(-lambda);
int k = 0;
double p = 1;
do {
k++;
// generate uniform random number u in [0,1] and let p ← p × u.
p *= double(rand()) / RAND_MAX;
} while (p > L);
return (k - 1);
}이미지의 각 픽셀 값은 영상신호를 만드는 CCD/CMOS 센서에서 노이즈가 포함된 전기신호(광자 수)의 평균값이 구현된 것으로 볼 수 있다. 따라서 영상에 Poisson 노이즈를 추가하는 과정은 역으로 주어진 픽셀 값을 평균으로 가지는 Poisson 분포의 램덤 변수를 픽셀값으로 대체하면 된다.(물론 이미지에 무관하게 노이즈를 추가할 수도 있다. 예를 들면 모든 픽셀에 대해서 같은 평균값을 갖는 포아송 노이즈를 주는 경우다)

double AddPoissonNoise(CRaster& raster, CRaster& noised) {
if (raster.IsEmpty()) return -1;
CSize sz = raster.GetSize();
int channel = raster.GetBPP() / 8;
noised = raster;
srand(unsigned(time(0)));
for (int y = 0; y < sz.cy; y++) {
BYTE *p = (BYTE *)raster.GetLinePtr(y);
BYTE *q = (BYTE *)noised.GetLinePtr(y);
for (int x = 0; x < sz.cx; x++)
for (int i = 0; i < channel; i++) {
int a = PoissonValue(*p++);
*q++ = a > 0xFF ? 0xFF: a;
}
}
return PSNR(raster, noised);
}
double PSNR(CRaster& raster, CRaster& noised) {
ASSERT(raster.GetBPP() == noised.GetBPP());
ASSERT(raster.GetSize() == noised.GetSize());
CSize sz = raster.GetSize();
int channel = raster.GetBPP() / 8;
double mse = 0; // mean-squared error;
for (int y = 0; y < sz.cy; y++) {
BYTE *p = (BYTE *)raster.GetLinePtr(y);
BYTE *q = (BYTE *)noised.GetLinePtr(y);
for (int x = 0; x < sz.cx; x++)
for (int i = 0; i < channel; i++) {
int a = *p++ - *q++;
mse += a * a;
}
}
mse /= (channel * sz.cx * sz.cy);
double decibel = 10. * log10(255 * 255 / mse);
return decibel;
};아래 예제는 cos(t)로 표현되는 신호에 Poisson noise를 주는 경우를 보여준다. Poisson noise 함수는 신호값을 평균으로 주는 event의 횟수를 찾아주므로 음수의 신호는 바로 다룰 수 없다. 따라서 원신호에 +1 만큼 더해 준 신호를 기준으로 한다. 그런데 cos(t) + 1의 범위가 [0,2]이므로 이산분포인 Poisson 분포를 적용하기 위해서는 적당한 스케일링이 필요하다. 예를 들면 cos(t) + 1이 신호의 절댓값을 측정한 것이 아닌 상대적인 세기를 나타내고, 실제 신호의 최댓값은 50으로 주어졌다면 Poisson noise을 만들 때 평균값이 주어진 신호 함수의 50배인 경우에 해당하는 값을 입력으로 넣은 후 출력값을 다시 50으로 나누어주면 된다.
void PoissonNoiseEx1D() {
FILE *fp = fopen("poisson.txt", "w");
for (double t = 0; t < 10; t += 0.01) {
double y = cos(t) + 1.;
fprintf(fp, "%f %f %f\n", t, y, (double)PoissonValue(y * 50) / 50.);
}
fclose(fp);
}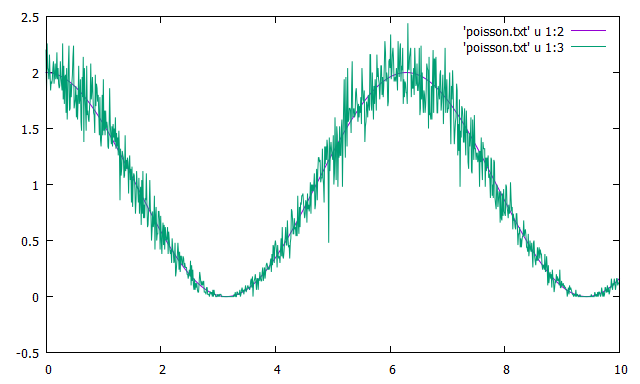
Poisson 잡음은 random noise처럼 단순히 더해지는 잡음과 달리 신호값이 클 때 잡음도 더 커짐을 알 수 있다. 그러나 SNR은 신호값이 클수록 더 좋아진다.
'Image Recognition > Fundamental' 카테고리의 다른 글
| Fowler Angle (0) | 2021.04.05 |
|---|---|
| Brute-Force Euclidean Distance Transform (0) | 2021.03.14 |
| Grassfire Algorithm (0) | 2021.03.05 |
| Image Sharpness (0) | 2021.02.25 |
| Selection Sort (0) | 2021.02.25 |




