Savitzky-Golay Smoothing Filter

The Savitzky–Golay method essentially performs a local polynomial regression (of degree $k$) on a series of values (of at least $k+1$ points which are treated as being equally spaced in the series) to determine the smoothed value for each point.

Savitzky–Golay 필터는 일정한 간격으로 주어진 데이터들이 있을 때(이들 데이터는 원래의 정보와 노이즈를 같이 포함한다), 각각의 점에서 주변의 점들을 가장 잘 피팅하는 $k$-차의 다항식을 최소자승법으로 찾아서 그 지점에서의 출력값을 결정하는 필터이다. 이 필터는 주어진 데이터에서의 극대나 극소, 또는 봉우리의 폭을 상대적으로 잘 보존한다.(주변 점들에 동등한 가중치를 주는 Moving Average Filter와 비교해 볼 수 있다).

간단한 예로, 2차의 다항식과 5개의 데이터 점

$$\{(-2,d_0),(-1,d_1),(0,d_2),(1,d_3),(2,d_4)\}$$

을 이용해서 중앙에서의 값을 결정하는 방법을 살펴보자. 사용하려고 하는 다항식은

$$p(x)=a_0+a_{1}x+a_2{x}^2$$

이다. 다항식의 계수는 다항식의 값과 실제 데이터의 값과의 차이를 최소화시키도록 선택해야 한다. 즉, 최소자승의 원리를 적용하여서 구하면 된다. 계산된 다항식의 값과 실제 데이터 값 사이의 차의 제곱을 구하면:

$$L=|a_0-2a_1+4a_2-d_0{|}^2+|a_0-a_1+a_2-d{|}^2+|a_0-d_0{|}^2$$ $$+|a_0+a_1+a_2-d_3{|}^2+|a_0+2a_1+4a_2-d_4{|}^2$$

이 식의 $a_0,a_1,a_2$에 대한 극값을 가질 조건은($\partial L/\partial a_i=0$) $$5a_0+10a_2=d_0+d_1+d_2+d_3+d_4$$$$10a_1=-2d_0–d_1+d_3+2d_4$$$$10a_0+34a_2=4d_0+d_1+d_3+4d_4$$

이 식을 만족시키는 $a_0$를 구하면, 필터의 출력(원도 중앙에서 값)이 결정된다.

$$\text{필터 출력:}{a}_0=(-3d_0+12d_1+17d_2+12d_3-3d_4)/35$$

위에서 계수 $a_0$, $a_1$, $a_2$를 결정하는 방정식은 행렬로 정리하면 아래의 식과 같이 표현할 수 있다. 

좌변의 5행 3열 행렬을 $\mathbf{A}$, $\mathbf{a}=[a_0,a_1,a_2{]}^T$, $\mathbf{d}=[d_0,d_1,d_2,d_3,d_4{]}^T$로 놓으면, 이 행렬방정식은 $\mathbf{A}\mathbf{.}\mathbf{a}\mathbf{=}\mathbf{d}$ 형태로 쓸 수 있다. $\mathbf{A}$(design matrix)가 정방행렬이 아니므로 역행렬을 바로 구할 수 없지만, $|\mathbf{A}\cdot \mathbf{a}\mathbf{-}\mathbf{d}{|}^2$을 최소로 하는 최소제곱해는
$$\mathbf{(}{\mathbf{A}}^{\mathbf{T}}\cdot \mathbf{A}\mathbf{)}\cdot \mathbf{a}\mathbf{=}{\mathbf{A}}^{\mathbf{T}}\cdot \mathbf{d}$$를 만족시켜야 하므로 

$$\mathbf{a}\mathbf{=}\mathbf{(}{\mathbf{A}}^{\mathbf{T}}\cdot \mathbf{A}{\mathbf{)}}^{\mathbf{-}\mathbf{1}}\cdot \mathbf{(}{\mathbf{A}}^{\mathbf{T}}\cdot \mathbf{d}\mathbf{)}$$로 주어짐을 알 수 있다.

이 식은 임의의 $k$-차 다항식을 이용한 경우에도 사용할 수 있다. 이 경우 행렬(scattering matrix) ${\mathbf{A}}^{\mathbf{T}}\cdot \mathbf{A}$는 $(k+1)\times (k+1)$의 대칭행렬이 된다. 행렬 $\mathbf{A}$는 다항식의 찻수와 피팅에 사용이 될 데이터의 구간의 크기가 주어지면 정해지므로, 윗 식에서 $({\mathbf{A}}^T\cdot \mathbf{A}{)}^{-1}\cdot {\mathbf{A}}^T$의 첫 행 ($a_0$을 $d$로 표현하는 식의 계수들)을 구하면 코드 내에서 결과를 lookup table로 만들어서 사용할 수 있다. 아래 표는 mathematica 를 이용해서 윈도 크기가 7 (7개 점)인 경우 2차 다항식을 사용할 때 계수를 구하는 과정이다.

 

2차 다항식일 때, 같은 방식으로 다양한 윈도 크기에 따른 계수를 구할 수 있다.
*크기($n$)에 따른 필터값 결정계수 (중앙에 대해 좌우대칭이다);

$$\begin{array}{rl}n=5;& W[]=\{-3,12,\mathbf{17},12,-3\};\\ n=7;& W[]=\{-2,3,6,\mathbf{7},6,3,-2\};\\ n=9;& W[]=\{-21,14,39,54,\mathbf{59},54,39,14,-21\};\\ n=11;& W[]=\{-36,9,44,69,84,\mathbf{89},84,69,44,9,-36\};\\ n=13;& W[]=\{-11,0,9,16,21,24,25,24,21,16,9,0,-11\}\\ n=15;& W[]=\{-78,-13,42,87,122,147,162,167,162,147,122,87,42,-13,-78\}\\ n=25;& W[]=\{-253,-138,-33,62,147,222,287,342,387,422,447,462,467,\\ & 462,447,422,387,342,287,222,147,62,-33,-138,-253\}\end{array}$$

$$\text{필터 출력}=\frac{\sum _{i}W[i]d[i]}{\sum _{i}W[i]}$$

std::vector<double> SavitzkyGolayFilter(std::vector<double>& data, double W[], int wsz) {
    const int hwsz = wsz >> 1;
    wsz = (hwsz<<1) + 1;
    std::vector<double> padded(data.size() + 2 * hwsz);
    // reflective boundary conditions;   
    // [hw]...[1][0][1][2]...[hw]....[n-1+hw][n-2+hw][n-3+hw]....[n-1];
    for (int i = 0; i < hwsz; i++) { 
        padded[i]                  = data[hwsz-i];
        padded[i+data.size()+hwsz] = data[data.size()-2-i];
    }
    for (int i = data.size(); i-->0;) padded[i+hwsz] = data[i];
    //
    std::vector<double> smoothed(data.size());
    double wsum = 0;
    for (int i = 0; i < wsz; i++) wsum += W[i]; 
    for (int i = data.size(); i-->0;) {
        double *ppad = &padded[i];
        double fsum = 0;
        for (int k = 0; k < wsz; k++) fsum += ppad[k] * W[k];
        smoothed[i] = fsum / wsum;
    }
    return smoothed;
};

$$f(x)=1-(|x|+0.01{)}^{0.01}+N(0,0.002),-2\le x\le 2$$

25 points

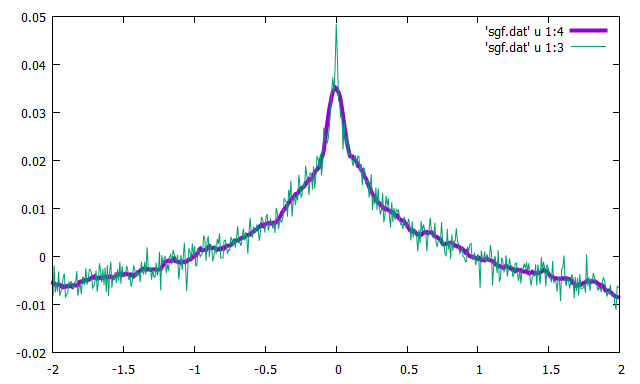
일반적인 찻수(order)에 대한 필터 계수 계산;

std::vector<double> sgFilterCoeffs(int width, int order/* = 2*/) {
    // ASSERT(width >= order+1);
    int hwidth = width >> 1;
    width = (hwidth << 1) + 1; // width = odd number;
    // design matrix;
    std::vector<double> D((order+1) * width);
    for (int i = 0; i < width; i++) {
        double x = double(i) - hwidth;  // -hwidth <= x <= hwidth;
        double *pD = &D[i*(order+1)];
        pD[0] = 1;
        for (int k = 1; k <= order; k++) 
            pD[k] = pD[k-1] * x;
    };
    // scattering matrix;
    std::vector<double> S((order+1)*(order+1)); // S=~D.D;
    for (int i = 0; i <= order; i++)
        for (int j = i; j <= order; j++) {
            double s = 0;
            for (int k = 0; k < width; k++)
                s += D[k*(order+1) + i] * D[k*(order+1) + j];
            S[i*(order+1) + j] = s;
        }
    for (int i = 0; i <= order; i++) 
        for (int j = 0; j < i; j++) 
            S[i*(order+1) + j]= S[j*(order+1) + i];
			
    // ccmath library;
    psinv(&S[0], order+1);
    // filter coeffs = 0-th row fo S.~D;
    std::vector<double> filter;
    for (int i = 0; i < width; i++) {
        double s = 0;
        for (int k = 0; k <= order; k++)
            s += S[k] * D[i*(order+1) + k];
        filter.push_back(s);
    }
    return filter;
}