마찰이 없는 표면으로 구성된 돔의 꼭대기에 입자를 올려져 있다고 하자. 외부에서 충격이 주어지지 않는 이상 입자는 영원히 꼭대기에 그대로 있을 것이고, 꼭대기에서 살짝 벗어나게 충격을 주면 중력 때문에 입자는 돔 표면을 따라 아래로 미끄러지는 운동을 시작할 것이다. 이제 다음 식으로 표현된 곡선을 회전했을 때 만들어지는 돔이 고려하자.
$$ y = \frac{2b^2}{3g} s^{3/2}$$
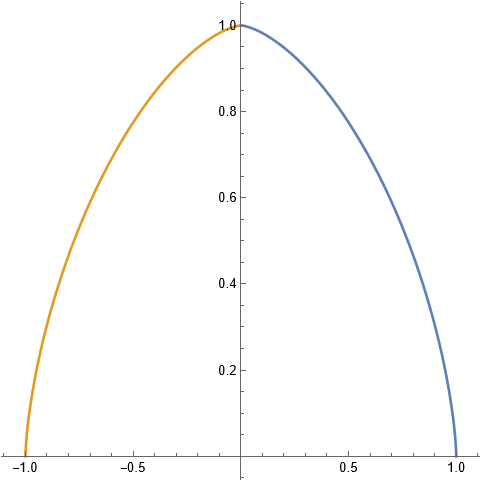
여기서 $y$는 꼭대기에서 표면의 한 지점까지 수직방향으로 내려간 거리고, $s$는 그 지점까지 돔표면을 따라 이동하는 최단거리, 그리고 $b$는 돔의 모양을 결정하는 변수이다. 돔의 표면에서 움직이는 입자는 처음 수직축에 대한 각운동량을 가지지 않았다면 돔의 대칭성 때문에 꼭대기를 기준으로 자른 단면에 그려진 곡선을 따라 움직일 것이다.
이제 물체가 돔 표면을 따라 움직이는 거리 $s$가 만족하는 방정식을 뉴턴의 운동방정식으로부터 구해보자. 속도나 가속도는 시간 $t$의 함수로도 생각할 수 있고, 또 움직인 거리 $s$의 함수로도 생각할 수 있다. 물체의 속도는
$$\vec{v} = \frac{d\vec{r}} {dt} = \frac{ds}{dt} \frac{d \vec{r}}{ds} = v \vec{T},~~~~ v=|\vec{v}| = \frac{ds}{dt},~\vec{T}= \frac{d\vec{r}}{ds} $$
그리고 가속도는
\begin{align} \vec{a} = \frac{d \vec{v}}{dt} = \frac{d^2s}{dt^2 } \vec{T} + \left( \frac{ds}{dt}\right)^2 \frac{d\vec{T}}{ds}\end{align}로 표현되는데, $|\vec{T}|=1$이므로 $d\vec{T}/ds$는 $\vec{T}$에 수직이다. 이 수직방향의 단위벡터를 $\vec{N}$으로 하면 $$\frac{d\vec{T}}{ds}= \kappa \vec{N}$$처럼 쓸 수 있는데, $\kappa$는 그 지점에서 곡선의 곡률을 의미한다. 곡선이 반지름 $R$인 원인 경우 $\kappa = 1/R$임을 보일 수 있다. 즉 가속도는 물체 경로에 접선방향 성분과 수직방향선으로 분해할 수 있다.
$$ \vec{a} = \ddot{s} \vec{T} + \kappa \dot{s} ^2 \vec{N}$$
곡선의 접선방향이 수평과 이루는 각을 $\theta$라면 물체에 작용하는 접선방향 중력성분이 $mg \sin \theta$이므로 운동방정식의 접선성분을 쓰면
$$ m \ddot{s} = mg \sin \theta $$
그리고 $\tan \theta = dy/dx$ 이므로 $ds^2 = dx^2+ dy^2$ 에서 $\sin\theta$를 구체적으로 곡선길이로 표현할 수 있다:
$$ \sin \theta = \frac{dy}{ds} = \frac{b^2 }{g} \sqrt{s}$$ 따라서 접선방향 운동방정식에 다음 식으로 표현되는 곡선길이에 대한 미분방정식을 얻을 수 있다. $$ \ddot{s} = b^2 \sqrt{s}$$
처음 돔의 꼭대기에 물체가 가만히 놓인 경우 초기조건은
$$ s(0) = 0,\quad v(0)=\dot{s}(0) = 0$$이다. $s(t) = 0$은 당연히 운동방정식과 초기조건을 만족시킨다. 즉, 처음 돔 꼭대기에 초기속도 없이 놓인 물체는 영원히 그 위치에 머물게 된다. 그런데 이 방정식은 위에서 구한 trivial 해 이외에도 임의의 양의 실수 $\epsilon>0$에 대해 다음과 같은 함수도 해가 될 수 있음을 쉽게 확인할 수 있다.
$$ s(t) = \left\{ \begin{matrix} 0 & t \le \epsilon \\ \frac{1}{144} \left[ b(t- \epsilon) \right]^4 & t > \epsilon \end{matrix} \right.$$
이는 주어진 초기조건을 만족하는 해가 무수히 많이 존재함을 의미한다. 꼭대기에 놓여진 물체가 외부의 요동이 없이도 자발적으로 운동이 가능하다는 이 해의 존재는 결정론적 뉴턴역학 체계에 비결정론적 시스템이 있을 수 있다는 예를 보여준다. 이를 dome paradox 또는 처음 발견한 Norton's dome 문제라고 부른다.
수학적으로는 Dome 에서 경로가 Lipschitz 조건을 만족시키지 못하기 때문에 주어진 초기조건을 만족시키는 미분방정식의 해가 유일할 필요가 없기 때문이다. Lipschitz 조건을 만족시키기 위해서 조금 떨어진 두 지점에서 함수값이 일정 이상 비율로 차이가 나지 않아야 되는데, 위의 식으로 표현된 돔은 원점에서 곡률이 발산하므로 Lipschitz 조건을 만족시킬 수 없다.
참고: Norton, John D. (November 2003). "Causation as Folk Science". Philosophers' Imprint. 3 (4): 1-22.
'Mathematics' 카테고리의 다른 글
| 단위구에서 거리에 대한 확률밀도함수(distribution of distance in a unit ball) (0) | 2025.02.07 |
|---|---|
| 단위원 내부점 사이의 평균 거리(mean distance between two points in a circular disk) (0) | 2025.02.07 |
| 단위구 내부점 사이의 평균 거리(mean distance between 2 points in a ball) (0) | 2025.02.06 |
| 단위구 내부점 사이의 평균 거리역수(mean reciprocal distance between points in a unit ball) (0) | 2025.02.04 |
| 쌍곡선의 반사특성(Reflective Property of Hyperbola) (5) | 2025.01.26 |




