열방정식은 매질에서 열이 전달되는 과정을 기술한다. 열은 온도차이가 있을 때 전달되는 에너지로 온도 분포 $u(\vec{r},t)$가 주어진 경우 주변으로 나가는 열에너지는 온도의 gradient $\nabla u$에 비례한다.
$$ \text{heat flux: }\quad \vec{j}= \kappa (u)\nabla u$$
$\kappa$는 매질에서 열이 얼마나 잘 전도는지를 표현하는 일반적으로 $u$에 의존할 수 있다. 균일하고 등방적인 매질인 경우는 $\kappa$가 일정한 상수에 해당한다. 국소적으로 단위부피당 단위시간당 빠져나가는 열에너지는 thermal flux의 divergence에 비례하고 이 값이 0이 아니면 그 지점의 온도 변화를 만든다. 따라서 온도는 다음과 같은 방정식을 만족한다.
$$ u_t = \nabla \cdot \vec{j} = \nabla\cdot(\kappa \nabla u)$$
이 방정식은 물질의 확산 현상에도 적용이 가능한데 이 경우 $u$는 물질의 밀도분포에 해당할 것이다.
$\kappa$가 상수인 경우 이 방정식은 선형방정식으로 초기 온도분포 $u(x,t=0)=f(x)$가 주어지면 해는 사이즈가 $\sigma = \sqrt{2\kappa t}$인 가우시안 커널(heat kernel 또는 Greeen function)과 초기 온도분포의 convolution으로 표현할 수 있다. 1차원 선형 열방정식의 해는 구체적으로 다음과 같이 표현된다.
\begin{align} u(x,t) = \int \frac{1}{\sqrt{4\pi \kappa t}} e^{- (x-y)^2 / 4\kappa t } f(y) dy = ( G_{\sigma} * f)(x,t)\\G_\sigma (x) = \frac{1}{\sqrt{2\pi\sigma} } e^{- x^2/2\sigma^2} \end{align}
열방정식은 뜨거운 커피가 담긴 잔을 방에 놓았을 때 방 안의 온도가 어떻게 변할지도 알 수 있게 해 준다. 물론 경험적으로 커피의 온도는 내려가고 방안은 잔의 주변부터 점차로 데워져서 나중에서는 모든 부분이 일정한 온도를 가지는 평형상태에 도달한다. 이는 가우시안 커널의 크기가 $\sqrt{t}$에 비례하므로 시간이 흐를수록 모든 지점에서 온도는 일정한 값으로 수렴할 것임을 쉽게 예측할 수 있다.
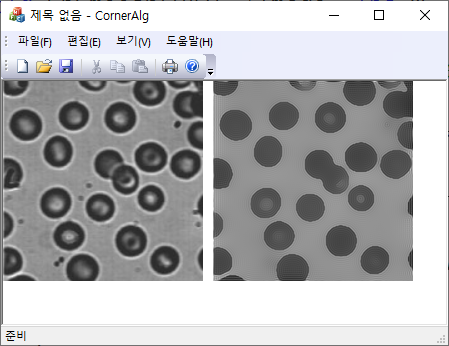
이 열방정식을 이미지에 대해서도 적용할 수 있다. 이 경우 초기 온도분포는 주어진 이미지의 명암값에 해당한다. 열방정식의 우변을 이미지에 적용하면 Gaussian 블러링에 해당하고, 시간은 블러링의 순차적인 적용 횟수를 의미한다. 이미지가 블러링 되는 경우 영상이 담고 있는 정보는 점점 잃게 되는데 이를 방지하기 위해서는 영상의 에지 정보를 보존하는 방법으로 열방정식을 변형시켜 보자. 영상에서 에지영역에서는 gradient 값이 커지므로 이 지점에서는 커널사이즈를 작게 (열방정식 관점에서는 열전도도를 줄임) 만들면 블러링 효과가 줄어들게 된다. 이를 위해서 다음과 같은 열전도도 함수를 도입하자.
$$ \kappa (u) = \frac {1}{1+ |\nabla u|^2/\lambda^2 }$$
여기서 $\lambda$은 contrast 파라미터로 에지의 세기가 $|\nabla| \gg \lambda$ 영역에서는 블러링의 영향을 거의 받지 않게 되어 열방정식을 적용하더라도 에지에 대한 정보 손실은 거의 일어나지 않는다. 그러나 $\kappa $가 상수가 아닌 경우는 열방정식은 비선형이므로 해를 명시적으로 쓸 수 없고 오직 수치해석적으로만 구할 수 있다.
먼저 미분연산자(Sobel operator: $\lambda$의 설정은 미분연산자의 normalization을 고려해야 함)을 이용해서 이미지의 gradient을 구하면 flux $\vec{j}$을 구할 수 있고, 다시 $j_x$에 대해서 $x-$방향 미분, $j_y$에 대해서 $y-$방향 미분을 해서 $\vec{j}$의 divergence, 즉 이미지의 일반화된 Laplace 연산 결과를 얻을 수 있다. 이 결과에 시간간격을 곱한 양을 이전 이미지에 더하여 새로운 이미지를 얻는다. 이 과정을 반복적으로 수행하면 된다.
$$ u(x,y, t+\Delta t) = u(x, y, t) + \Delta t \times \nabla \cdot (\kappa (|\nabla u| ) \vec{j})$$
$\kappa$가 상수일 때 $t \to \kappa t$로 시간변수를 바꾸면 열방정식은 차원이 없는 형태로 되고, $\kappa <1$이므로 시간간격은 $\Delta t \ll 1$를 만족하도록 선택해야 한다.

double conductivity(double gmagsq, double lambdasq) {
return 1.0/ (1.0 + gmagsq/lambdasq);
}
int LaplaceImage(double *img, int w, int h, double lambda, double *laplace) {
const double lambdasq = lambda * lambda;
// Sobel gradient 3x3
const int nn[] = { -w - 1, -w, -w + 1, -1, 0, 1, w - 1, w, w + 1};
const int sobelX[] = { -1, 0, 1, -2, 0, 2, -1, 0, 1};
const int sobelY[] = { -1, -2, -1, 0, 0, 0, 1, 2, 1};
std::vector<double> Gx(w * h, 0);
std::vector<double> Gy(w * h, 0);
std::vector<double> Gmag2(w * h, 0);
const int xmax = w - 1, ymax = h - 1;
// gradient-x, gradient-y, and mag of gradient.
for (int y = 1, pos = w; y < ymax; y++) { // pos = w; starting address;
pos++; //skip x=0;
for (int x = 1; x < xmax; x++, pos++) {
double sx = 0, sy = 0;
for (int k = 0; k < 9; k++) {
double v = img[pos + nn[k]];
sx += sobelX[k] * v;
sy += sobelY[k] * v;
}
Gx[pos] = sx;
Gy[pos] = sy;
// gx^2 + gy^2;
Gmag2[pos] = sx * sx + sy * sy;
}
pos++; // skip x=xmax;
}
// flux;
for (int y = 1, pos = w; y < ymax; y++) { // pos = w; starting address;
pos++; //skip x=0;
for (int x = 1; x < xmax; x++, pos++) {
double kappa = conductivity(Gmag2[pos], lambdasq);
// multiply conductivity;
Gx[pos] *= kappa;
Gy[pos] *= kappa;
}
pos++; // skip x=xmax;
}
// divergence -> laplace;
for (int y = 1, pos = w; y < ymax; y++) { // pos = w; starting address;
pos++; //skip x=0;
for (int x = 1; x < xmax; x++, pos++) {
double sx = 0, sy = 0;
for (int k = 0; k < 9; k++) {
sx += sobelX[k] * Gx[pos + nn[k]];
sy += sobelY[k] * Gy[pos + nn[k]];
}
laplace[pos] = sx + sy;
}
pos++; // skip x=xmax;
}
return 1;
}
void EpSmooth(BYTE *image, int w, int h, BYTE *out) {
const double lambda = 50.0;
const double dt = 0.01; //time step;
const int maxiter = 100;
std::vector<double> fimage(w * h, 0);
std::vector<double> laplace(w * h, 0);
for (int k = fimage.size(); k-- > 0;) fimage[k] = image[k];
for (int iter = maxiter; iter-- > 0;) {
LaplaceImage(&fimage[0], w, h, lambda, &laplace[0]);
// update image;
for (int k = fimage.size(); k-- > 0; )
fimage[k] += dt * laplace[k];
}
// preparing output;
for (int k = fimage.size(); k-- > 0; ) {
int a = int(fimage[k]);
out[k] = a > 255 ? 255: a < 0 ? 0: a;
}
}'Image Recognition' 카테고리의 다른 글
| Image Matting: Knockout method (1) | 2024.07.16 |
|---|---|
| Anisotropic Diffusion Filter (2) (0) | 2024.02.23 |
| Watershed Segmentation (0) | 2021.02.27 |
| Local Ridge Orientation (0) | 2021.02.21 |
| Contrast Limited Adaptive Histogram Equalization (CLAHE) (3) | 2021.02.15 |




