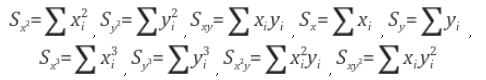최소 자승법 문제는 추정치와 실제의 측정치와의 차이를 최소로 만드는 parameter vector를 구하는 것이다.
$$\underset{\mathbf{x}} {\text{argmin}} ~|\mathbf{A}. \mathbf{x} - \mathbf{b}|^2.$$
여기서 design matrix $\mathbf{A}$는 추정에 사용이 된 basis 함수를 각각의 독립변수에서 계산한 값이고, $\mathbf{x}$는 구하고자 하는 parameter vector이며, $\mathbf{b}$는 측정값 vector이다. 예를 들면 주어진 측정값을 $n-1$차의 다항식을 이용하여서 피팅하려고 하는 경우에는 parameter는 다항식의 계수가 되며 $n$-차원의 vector space을 형성하게 되며, $\mathbf{A}$는
$$ A_{ij} = (x_i)^j , \quad j=0,..., n-1$$
가 일 것이다. 일반적으로 $A_{ij}$는 $x_i$에서 계산된 basis-함수의 값이 된다. 위의 식을 $\mathbf{x}$에 대해서 미분을 하면 극값을 취하면 최소자승 문제는 아래의 행렬식을 푸는 문제가 된다
$$ (\mathbf{A}^T. \mathbf{A}) .\mathbf{x} = \mathbf{A}^T. \mathbf{b}.$$
$\mathbf{A}^T. \mathbf{A}$ 은 $n\times n$ matrix다. 이 행렬이 역행렬을 가지게 되면
$$ \mathbf{x} = (\mathbf{A}^T. \mathbf{A})^{-1} . (\mathbf{A}. \mathbf{b}),$$
를 하여서 원하는 parameter vector를 얻을 수 있다. 그러나 피팅 문제에 따라 행렬 $\mathbf{A}^T. \mathbf{A}$가 매우 singular 해져 역행렬을 구할 수 없게 되는 경우에 종종 생긴다. 예를 들면, 저주파의 신호를 고주파 기저 함수를 이용하여서 최소자승법을 사용하고자 하는 경우 등에 이러한 문제에 부딪히게 된다. 이런 경우에는 직접적으로 $\mathbf{A}^T. \mathbf{A}$의 역행렬을 구하는 방법을 이용할 수 없고
$$ \mathbf{A} .\mathbf{x} = \mathbf{b}$$
의 식을 $\mathbf{A}$의 SVD(Singular Value Decomposition)를 이용하여서 풀 수가 있다. $\mathbf{A}$를 SVD 하면 $\mathbf{A}_{m\times n}=\mathbf{U}_{m\times n} . \mathbf{w}_{n\times n}. \mathbf{V}_{n\times n}^T $의 형태로 분해할 수 있다. 여기서 $\mathbf{w}=\text{diag}(\underbrace{w_0, w_1,...}_{\text{nonzero}},0,..,0)$로 쓰여지는 대각행렬이다. matrix $\mathbf{U}$와 $\mathbf{V}$의 column vector를 사용하면
$$ \mathbf{A} =\sum_{w_k \ne 0} w_k \mathbf{u}_k \otimes \mathbf{v}_k^T$$
의 형태로 쓰인다. $\mathbf{u}_k$는 $\mathbf{U}$의 $k$-번째 열벡터이고, $\mathbf{v}_k$는 $\mathbf{V}$의 $k$-번째 열벡터로 각각 orthonormal basis를 형성한다. parameter 벡터를 $\{ \mathbf{v}_k \}$ basis로 전개를 하면 영이 아닌 singularvalue에 해당하는 성분만 가지게 된다. 구체적으로 위의 $\mathbf{A}$ 분해와 $\mathbf{u}_j^T.\mathbf{u}_k=\delta_{jk}$, 그리고 $\sum_k \mathbf{v}_k \otimes \mathbf{v}_k^T= \mathbf{I}_{n\times n}$임을 이용하면,
\begin{gather} \mathbf{v}_k^T . \mathbf{x} = \mathbf{u}_k^T . \mathbf{b} / w_k, \quad w_k \ne 0, \\ \mathbf{v}_k^T . \mathbf{x} = 0, \quad w_k = 0, \\ \rightarrow ~~\mathbf{x} = \sum _{w_k \ne 0 } ( \mathbf{u}_k^T . \mathbf{b} / w_k) \mathbf{ v} _k , \end{gather}
이어서 위의 해를 구할 수 있다. 이 해는 $|\mathbf{A} . \mathbf{x} - \mathbf{b}|^2$를 최소화한다.
int svd(double *A, int m, int n, double* w, double *V); // from cmath libary.
void fit_func(double x, double val[], int n) { // polynomial fitting sample;
val[0] = 1;
for(int i = 1; i < n; ++i)
val[i] = x * val[i - 1];
}
#define EPSILON 1.E-8
int svd_fit(const double x[], const double y[], const int m, const int n,
void (*fit_func)(double , double [], int ),
double params[],
double *error)
{
double *A = new double [m * n];
double *w = new double [n];
double *V = new double [n * n];
// evaluate design matrix;
for (int i = 0; i < m; ++i)
fit_func(x[i], &A[i * n + 0], n) ;
svd(A, m, n, w, V);
// now A becomes U matrix;
// truncate small singular values;
double wmax = 0;
for (int i = 0; i < n; ++i)
if (w[i] > wmax) wmax = w[i];
double thresh = wmax * EPSILON;
for (int i = 0; i < n; ++i)
if (w[i] < thresh) w[i] = 0;
// back substitution;
double *tmp = new double [n];
for (int j = 0; j < n; ++j) {
double s = 0;
if (w[j]) {
for (int i = 0; i < m; ++i)
s += A[i * n + j] * y[i];
s /= w[j];
}
tmp[j] = s;
}
for (int j = 0; j < n; ++j) {
double s = 0;
for (int jj = 0; jj < n; ++jj)
s += V[j * n + jj] * tmp[jj];
params[j] = s;
};
//estimate error;
*error = 0;
for (int i = 0; i < m; ++i) {
fit_func(x[i], &A[i * n + 0], n); //use A as a tmp buffer;
double sum = 0;
for (int j = 0; j < n; ++j) sum += params[j] * A[i * n + j] ;
double err = (y[i] - sum);
*error += err * err ;
}
delete[] A; delete[] w; delete[] V;
delete[] tmp;
return 1;
}
'Image Recognition > Fundamental' 카테고리의 다른 글
| Image rotation by FFT (0) | 2022.02.18 |
|---|---|
| FFT를 이용한 영상의 미분 (0) | 2022.02.12 |
| Color Histogram Equalization (4) | 2022.02.07 |
| Least Squares Fitting of Ellipses (0) | 2022.01.27 |
| Circle Fitting: Pratt (0) | 2022.01.20 |