초기의 지구는 매우 뜨거워 모든 암석들이 녹아있는 상태였을 것이다. 시간이 흐르면서 지구는 표면에서 차가운 우주(거의 0K이다)로 열이 배출되어 점차 식게 된다. 처음에서 표면과 내부의 온도가 같았지만 열의 배출과정에서 표면의 온도는 내부의 온도보다 낮게 되어 지구 내부에서 온도의 gradient가 만들어진다. 실험적으로 지표면 근처에서 이 기울기를 측정하면 지구 나이를 추정할 수 있다.
지구 내부에서 온도의 분포는 열방정식에 의해서 구할 수 있다. 우선 지구가 매우 크므로 평평한 판(그리고 매우 두꺼운)으로 근사를 하자. 그러면 열이 식는 과정은 1차원 열방정식으로 설명할 수 있다. 지구 내부 깊이 $x>0$인 지점에서 온도 분포 $u(x, t)$는 다음의 열방정식에 의해서 결정된다.
\begin{align} u_t(x, t) = \kappa u_{xx} (x,t), \quad u(x, t=0)=f(x), \qquad x>0\end{align}
여기서 $f(x)$는 초기 지구 내부 온도로 일정한 값으로 생각할 수 있다. 지표면 밖(우주)은 무한히 큰 차가운 열원으로 생각할 수 있으므로 온도가 $0\rm K$으로 고정되어 있다고 볼 수 있다. 즉, $u(x,t)$은 모든 시간에서 다음의 경계조건을 만족해야 한다.
$$ u(x=0, t)=0$$
이 $x\ge 0$에서 열방정식은 전체 실수구간에서의 열방정식을 푸는 문제로 변환하면 보다 쉽게 해결할 수 있다. 단, $x=0$에서 경곗값을 유지해야 하므로 $t=0$일 때 초기값은 원 문제의 기함수로 확장을 쓰면 된다. 물리적으로 $t=0$ 일 때 $x=0$을 기준으로 $T$와 $-T$(물론 음의 절대온도는 없다!)를 가지는 영역을 열접촉을 시키고 난 후의 온도 분포를 찾는 문제로 환원시킨 것과 같다. 따라서 다음의 열방정식의 해 $v(x,t)$를 우선 고려하자.
\begin{align} v_t (x,t) = \kappa v_{xx}(x,t), \quad v(x,0)= {f}_o(x)=\left\{ \begin{matrix} f(x) & x>0 \\ -f(-x) & x <0\end{matrix}\right. \end{align}
이 방정식의 해는 다음처럼 써진다.(Fourier 변환과 convolution을 사용하면 쉽게 구할 수 있다). $\hat{v}(s,t)$와 $\hat{f_o}(s)$를 각각 $v(x,t)$와 ${f_o}(x)$의 공간에 대한 Fourier 변환이라면 열방정식은
$$\hat{v}_t (s,t)= -\kappa s^2 \hat{v}(s,t),\quad \hat{v}(s, 0) = \hat{f_o}(s)$$
$t$에 대해 적분하면 다음처럼 두 함수의 곱으로 표현된다.
\begin{align} \hat{v}(s,t) = e^{- \kappa s^2 t /2} \hat{f_o}(s) = \hat{K}(s,t) \hat{f_o}(s)\end{align}
따라서 $v(x,t)$는 heat kernel $K(x,t)$와 ${f}_o(s)$의 convolution으로 주어지는데, $e^{-\kappa s^2 t}$의 역변환이 $K(x,t)=\frac{1}{\sqrt{4\pi\kappa t}} e^{- x^2/4\kappa t}$이므로
\begin{align} v(x,t) &= (K * {f}_o)(x,t)\\ &=\frac{1}{\sqrt{ 4\pi\kappa t}} \int_{-\infty}^\infty e^{- (x-y)^2/4\kappa t } {f}_o(y) dy \\ &= \frac{1}{\sqrt{4\pi\kappa t}} \int_0^\infty \Big( e^{-(x-y)^2/4\kappa t} - e^{-(x+y)^2 / 4\kappa t} \Big) f(y)dy \end{align}
항상 $v(0,t) = 0$을 만족함을 쉽게 확인할 수 있다. 따라서 $x\ge 0$에서 $u(x,t) = v(x,t)$이다. 초기온도 분포가 일정한 ($f(x)=T$) 경우는 적분을 정리하면 error function으로 써짐을 알 수 있다.
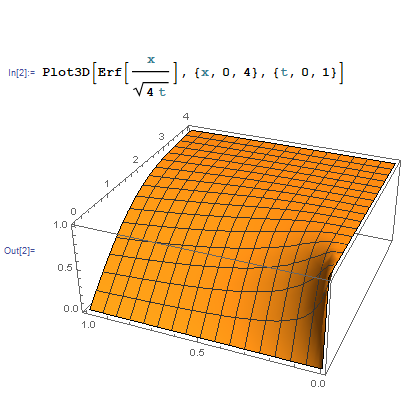
$$u(x,t) = \frac{T}{\sqrt{\pi \kappa t}} \int_0^x e^{-s^2 /4\kappa t } ds = T\times \text{Erf}(x/2\sqrt{\kappa t}) \quad (x\ge0)$$
현시점($t=t_0$)에서 $x=0$에서 온도 기울기 $\beta$를 구하면
$$\beta= u_x (0, t_0) = \frac{T}{\sqrt{\pi \kappa t_0}} \quad \rightarrow \quad t_0 = \frac{T^2}{\pi \kappa \beta^2} $$
지구 초기 온도로 $T = 3900 \rm K$, 지각의 평균 열확산도로 $\kappa = 1.2 \times 10^{-2} \rm cm^2/s$, 그리고 현시점의 지표면 근처에서 실험적으로 측정된 온도 기울기가 $\beta = 3.6\times 10^{-4} \rm K/cm$ 정도이므로
$$ t _0 =3.1131 \times 10^{15} \rm s = 9.7 \times 10^7 yr$$
이 추정에 의하면 지구나이가 1억 년이 안된다. 방사선 동위원소법에 의해서 지구 나이가 45억 년쯤 되는 것으로 나오는데 이와 큰 차이가 있다. 구형 지구를 고려하면 3차원 열방정식 문제가 되는데 이 방법을 쓰더라도 평평한 지구 모형을 쓴 결과와 큰 차이가 나지 않는다. 이는 지구가 생성된 이후 추가적인 열의 공급 없이 식는 과정만 고려한 모델인데 실제로는 지구내부에 있는 방사성 원소가 붕괴할 때 발생하는 열이 지속적으로 공급되고 있으므로 이에 대한 고려를 해야 좀 더 정확한 나이를 추정할 수 있을 것이다. 열방정식을 이용한 지구 나이 추정은 영국의 수리물리학자이자 공학자인 Kelvin 남작에 의해 시도되었다.
'Mathematics' 카테고리의 다른 글
| 수치적으로 보다 정밀한 이차방정식의 해 (0) | 2024.02.23 |
|---|---|
| 열방정식의 Green function (0) | 2024.02.12 |
| n 차원 공의 부피(Volume of an n Ball) (3) | 2024.02.07 |
| 타원의 둘레길이(Perimeter of an Ellipse) (2) | 2024.02.06 |
| 왜 땅속은 여름에 시원하고 겨울에는 따뜻한가? (1) | 2024.02.03 |



