구간 $[a=t_0, ...t_{n-1}=b]$에서 샘플링된 데이터 $\{ f_0, ...f_{n-1} \}$이 있다. $n-1$ 개의 각 구간에서 데이터를 보간하는 삼차다항식 함수 모임 $$S(t)= \{S_j (t)| t_j \le t <t_{j+1} , ~~j=0,1,2...,n-2 \} $$을 찾아보자. 전체 구간에서 연속적이고 충분히 부드럽게 연결되기 위해서는 우선 각 node에서 연속이어야 하고, 또한 1차 도함수와 2차 도함수도 연속이 되어야 한다. 물론 각 node에서는 샘플링된 데이터값을 가져야 한다.
\begin{align} (a) ~~& S(t_j) = f_j \\ (b)~~& S_{j+1}(t_{j+1}) = S_j( t_{j+1}) \\ (c)~~& S'_{j+1}(t_{j+1}) = S'_j(t_{j+1}) \\ (d)~~& S''_{j+1}(t_{j+1}) = S''_{j}(t_{j+1}) \end{align}
$n-1$개 구간에서 각각 정의된 3차 함수를 결정하려면 $4 \times (n-1)$개의 조건이 필요하다. (a)에서 $n$개, (b), (c), (d)에서 $3\times (n-2)$개의 조건이 나오므로 총 $n+3\times(n-2)=4n-6$개의 조건만 생긴다. 삼차식을 완전히 결정하기 위해서는 2개의 추가적인 조건을 부여해야 하는데 보통 양끝에서 2차 도함수값을 0으로 하거나(natural boundary) 또는 양끝에서 도함수 값을 특정한 값으로 고정시킨다(clamped boundary). 여기서는 양끝의 2차 도함수를 0으로 한 natural cubic spline만 고려한다. 그리고 $S_j(t)$가 $n-2$개의 구간에 대해서만 정의되어 있지만, 끝점을 포하는 구간에서도 정의하자. 이 경우 $S_{n-1}(t), t\ge t_{n-1}$에 부여된 조건은 $t_{n-1}$에서 $S_{n-2}(t)$와 연속, 미분연속 그리고 2차 도함수가 0인 조건만 부여된다.
$j-$번째 구간의 삼차함수를
$$S_j(t) = a_j + b_j (t - t_j) + c_j (t-t_j)^2 + d_j (t - t_j)^3$$
로 쓰고, 구간의 간격을
$$ h_j = t_{j+1} - t_j$$로 놓으면 (a)에서
$$ S_j (t_j) = a_j = f_i,~~ j=0,1,..n-2\qquad(a)$$
(b)에서
$$ a_{j+1} =a_j+ b_j h_j + c_j h_h^2 +d_j h_j^3,~~j=0,1,...,n-2 \qquad (b)$$
(c)에서
$$b_{j+1} = b_j + 2c_j h_j+ 3d_j h_j^2 ,~~j=0,1,...,n-2 \qquad (c) $$
(d)에서
$$ c_{j+1} = c_j+ 3d_j h_j ,~~j=0,1,...,n-2\qquad (d)$$
이므로 $d_j$에 대해서 푼 후 (b)와 (c)에 대입하면
$$ a_{j+1} = a_j + b_j h_j + \frac{h_j^2}{3} (2 c_j + c_{j+1}) \qquad (e)$$
$$ b_{j+1} = b_j + h_j (c_j + c_{j+1}) \qquad(f)$$
을 얻는다. 그리고 (e)에서 $b_j$에 대해서 풀면
$$ b_j =\frac{1}{h_j} (a_{j+1} - a_j) -\frac{h_j}{3} (2c_j + c_{j+1}) $$
$$ \to b_{j-1}=\frac{1}{h_{j-1}} (a_j - a_{j-1}) -\frac{h_{j-1}}{3}( 2c_{j-1} + c_j) $$
이 식을 index가 1씩 줄어든 (f)에 대입하면
$$ h_{j-1} c_{j-1} + 2(h_{j-1} + h_j) c_j + h_j c_{j+1}=\frac{3}{h_j}(a_{j+1}-a_j)-\frac{3}{h_{j-1}}(a_j -a_{j-1})$$$$~ j=1,2,...,n-2$$로 주어지는 $n$개의 계수 $c_j ~(j=0,1,...,n-1)$에 대한 선형연립방정식을 얻는다. 물론 매개변수 구간 간격 $h_j~(j=0,1,...,n-2)$와 spline의 상수항 $a_j~(j=0,1,2,...,n-2)$은 입력점으로 주어진다. 나머지 두 개의 조건은 양끝점에서 이차미분값을 0으로 설정하여 얻을 수 있다:
$$ S''(t_{n-1}) = 0\quad \to \quad c_{n-1}=0$$
$$ S''(t_0) = 0\quad \to \quad c_0 = 0$$
연립방정식을 ${\bf c}=\{c_j\}$에 대한 행렬방정식 형태 $\bf A \cdot x = b$로 정리하면 $n\times n$ 행렬 $\bf A$는 tridiagonal 모양이어서 쉽게 답을 구할 수 있다.
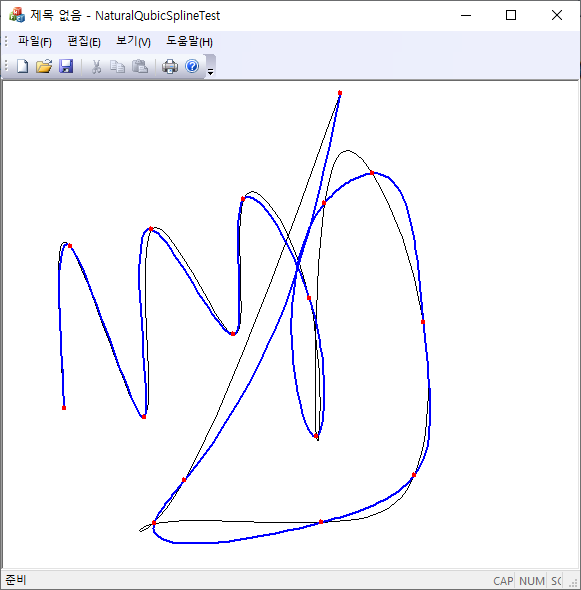
그림은 매개변수 구간 간격을 일정하게 잡았을 때(black)와 입력점 사이의 직선거리를 사용할 때(blue)의 차이를 보여준다.
std::vector<Cubic> cubicspline1(const std::vector<double>& a,
const std::vector<double>& h) {
const int n = a.size();
std::vector<double> w(n), l(n), m(n), z(n);
for (int i = n-1; i-->1;)
w[i] = 3 * (a[i + 1] - a[i]) / h[i] - 3 * (a[i] - a[i - 1]) / h[i - 1];
l[0]= 1; m[0] = 0; z[0] = 0;
for (int i = 1; i < n-1; i++) {
l[i] = 2 * (h[i] + h[i - 1]) - h[i - 1] * m[i - 1];
m[i] = h[i] / l[i];
z[i] = (w[i] - h[i - 1] * z[i - 1]) / l[i];
}
l[n-1] = 1;
z[n-1] = 0;
std::vector<double> c(n);
c[n-1] = 0;
std::vector<Cubic> spline(n-1);
for (int i = n-1; i-->0;) {
c[i] = z[i] - m[i] * c[i + 1];
double b = (a[i + 1] - a[i]) / h[i] - h[i] * (c[i + 1] + 2 * c[i]) / 3;
double d = (c[i + 1] - c[i]) / (3 * h[i]);
spline[i] = Cubic(a[i], b, c[i], d);
}
return spline;
}
// 매개변수가 균일하지 않는 경우임; 간격 = 입력점 직선거리;
std::vector<CPoint> NatCubicSpline(const std::vector<CPoint>& pts) {
if (pts.size() < 2) return std::vector<CPoint> (); //null_vector;
std::vector<double> ax(pts.size());
std::vector<double> ay(pts.size());
std::vector<double> h(pts.size()-1); // interval size;
for (int i = pts.size(); i-->0;) {
ax[i] = pts[i].x;
ay[i] = pts[i].y;
};
// parameter intervals;
for (int i = pts.size()-1; i-->0;) {
double dx = ax[i + 1] - ax[i];
double dy = ay[i + 1] - ay[i];
h[i] = hypot(dx, dy);
}
std::vector<Cubic> splinex = cubicspline1(ax, h);
std::vector<Cubic> spliney = cubicspline1(ay, h);
const int steps = 20;
std::vector<CPoint> curve;
curve.reserve(1 + splinex.size()*steps);
curve.push_back(pts.front());
for (int i = 0; i < pts.size()-1; i++) {
const double ds = h[i] / steps;
for (int k = 1; k <= steps; k++) {
const double tk = k * ds;
curve.push_back(CPoint(int(splinex[i].eval(tk) + 0.5),
int(spliney[i].eval(tk) + 0.5)));
}
}
return curve;
}'Computational Geometry' 카테고리의 다른 글
| Catmull-Rom Spline (2) (0) | 2024.06.21 |
|---|---|
| Minimum Volume Box (1) | 2024.06.16 |
| Polygon Decimation (0) | 2024.06.08 |
| Centripetal Catmull-Rom Spline (1) | 2024.06.06 |
| Bezier curves (1) | 2024.04.19 |



