$$ I = \int_{-1}^{1} \frac{ dx}{(1+x^2) \sqrt{1-x^2} } = \frac{ \pi}{\sqrt{2}}$$
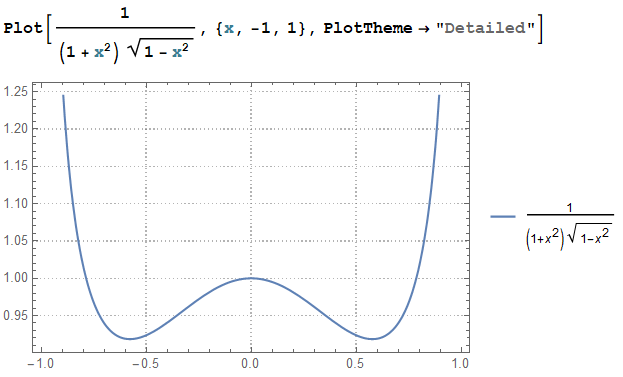
복소함수
$$ f(z) = \frac{1}{(1+z^2) \sqrt{1-z^2}}$$의 contour integral을 고려하자.

제곱근 함수때문에 branch cut을 잡아야 하는데, $-1 \le x \le 1$로 선택하자. 그러면 위상은 $0 \le \text{arg}(1-z) \le 2\pi$, $-\pi \le \text{arg}(z+1) \le \pi$로 설정될 수 있다.

그리고 $z=\pm i$는 $f(z)$의 simple로 residue는 $z=i$일 때
$$ z-1=\sqrt{2} e^{ i 3\pi/4} \to 1-z= \sqrt{2} e^{i 7\pi / 4}, ~z+1 = \sqrt{2} e^{i \pi / 4}\\ \to~~ \sqrt{1-z^2}= \sqrt{2} e^{i\pi} = -\sqrt{2} \\ \to \text{Res}f(z=i) = \frac{1}{-2i\sqrt{2}}$$그리고 $z=-i$에서는 $$ z-1= \sqrt{2} e^{i 5\pi/4} \to 1-z= \sqrt{2} e^{i \pi / 4}, ~z+1 = \sqrt{2} e^{-i\pi / 4} \\ \to~~ \sqrt{1-z^2}= \sqrt{2} e^{i 0} = \sqrt{2} \\ \to \text{Res}f(z=-i) = \frac{1}{-2i \sqrt{2}}$$
$C_1$ 경로에서 $z-1=(1-x)e^{i\pi} \to 1-z = (1-x) e^{i 2\pi}$, $z+1 = (1+x) e^{i 0}~(x:-1 \to 1)$이므로
$$ \int_{C_1} f(z) dz = \int_{-1}^1 dx \frac{dx}{(1+x^2) \sqrt{1-x^2} e^{ i\pi } } = - I $$
$C_2$ 경로에서 $z-1=(1-x) e^{i\pi} \to 1-z = (1-x) e^{i 0}$, $z+1 = (1+x) e^{i 0} ~(x: 1 \to -1)$이어서
$$ \int_{C_2} f(z) dz = \int_{1}^{-1} dx \frac{dx}{(1+x^2) \sqrt{1-x^2} e^{ i 0} } = - I $$
그리고 $C_\epsilon$, $C'_\epsilon$, $C_\infty$에서 적분값은 0에 수렴하므로 residue 정리에 의해서
$$ -2I = 2 \pi i \times \left( \frac{1}{-2i\sqrt{2}} + \frac{1}{-2i\sqrt{2}}\right)\qquad \to \qquad I = \frac{\pi}{\sqrt{2}}$$
'Mathematics' 카테고리의 다른 글
| Integration along a branch cut-027 (0) | 2024.10.15 |
|---|---|
| Integration along a branch cut-026 (0) | 2024.10.14 |
| Integration along a branch cut-024 (0) | 2024.10.07 |
| Integration along a branch cut-023 (1) | 2024.10.06 |
| Integration along a branch cut-022 (0) | 2024.10.05 |



