점전하 근처에 있는 도체구의 전위(potential at the surface of a conducting sphere near a point charge)
Physics/정전기 2025. 1. 22. 23:28반지름 $R$인 대전되지 않은 도체구가 있고 이 도체구의 중심에서 $d>R$만큼 떨어진 위치에 점전하 $Q$가 있다. 도체구의 전위는?

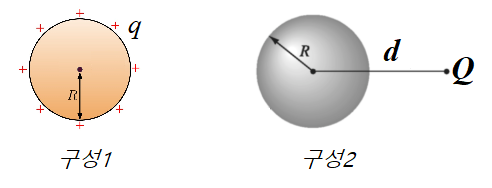
풀이: 영상전하법(method of image)을 사용하면 쉽게 구할 수 있다. 그렇지만 여기서도 Green's reciprocity theorem을 사용하자. 이를 이용하면 동일한 도체 구성에서 서로 다른 두 전하구성이 만드는 전위함수 사이에 하나의 관계를 얻을 수 있다. 우선 동일 구성에서 전위를 구할 수 있는 간단한 경우(구성-1)는 전하 $q$로 도체구로 대전시킨 경우다. 이 경우 전하분포와 전위함수는
$$ \sigma_1 = \frac{q}{4\pi R^2}=\text{const}$$
\begin{align} V_1 (r) = \left\{ \begin{matrix} \frac{q}{4\pi\epsilon_0 r} & r \ge R \\ \frac{1}{4\pi \epsilon_0 R} & r \le R\end{matrix} \right. \end{align}도체가 등전위임과 점전하를 도체구에 가까이 접근시킬 때 도체구 표면에서 전하분리가 일어나지만 총 전하량($=0$)은 변하지 않는다는 사실을 이용하면($\int_\text{sphere} \sigma_2 d^2x=0$),
$$ \int \rho_2 V_1 d^3x = Q \times V_1(d) + V_1 (R) \int_\text{sphere} \sigma_2 d^2x = Q \times V_1(d)$$또,$$ \int \rho_1 V_2 d^3x = q \times V_2(R)$$
이므로 우리가 구하려는 전하 구성의 경계에서 전위는
$$ V_2 (R) = \frac{Q }{ q }V_1(d) = \frac{Q}{4\pi \epsilon_0 d}$$ 즉, 도체구의 전위는 중심에서 점전하 $Q$ 단독의 전위와 같음을 알 수 있다. 왜 이런 값을 갖는가? 영상전하법으로 구할 때 점전하 $q$와 이의 영상전하가 만드는 전위가 도체 구면에서 0이므로(접지된 도체구일 때), 도체구가 일정한 전위를 가지기 위해서는 두 번째 영상전하를 중심에 놓아야 한다. 이 두 번째 영상전하의 크기는 도체구의 알짜 전하가 0이란 사실에 의해서 결정될 수 있는데 앞서 구한 전위는 이 두 번째 영상전하가 만드는 도체구면에서 전위와 같다.
'Physics > 정전기' 카테고리의 다른 글
| 평행판 축전기 외부에서 전기장은? (0) | 2025.01.23 |
|---|---|
| 대전된 구면에 생긴 구멍 중심에서 전기장의 세기는? (0) | 2025.01.23 |
| 극판에 모인 총전하는? (0) | 2025.01.22 |
| 구형축전기를 살짝 찌그리면 전기용량은 얼마나 변할까? (0) | 2024.08.29 |
| 도체구각의 전위는? (26) | 2023.11.24 |



