Geometry & Recognition

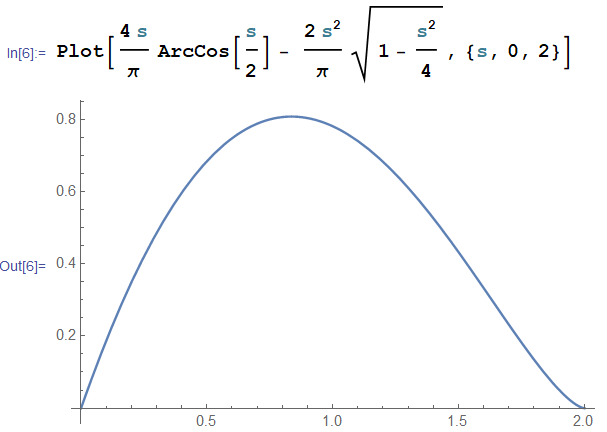
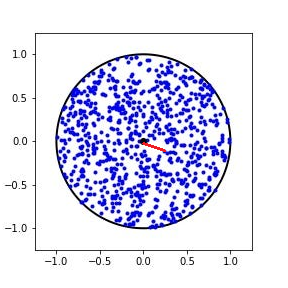
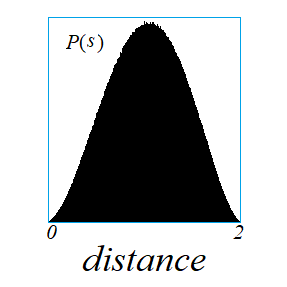
이전 포스팅(https://kipl.tistory.com/731)에서 단위구에서 두 점 사이거리의 평균을 구하는 과정에서 사이거리에 대한 확률밀도함수를 소개하였고, 또 단위원에서 사이거리에 대한 확률밀도함수를 구체적으로 구했다. 이제 단위원에서의 기법을 이용해서 단위구에서 사이거리 분포에 대한 확률밀도함수를 구하자. 두 저의 사이거리 $s$의 확률밀도함수는

$$ P(s) = \frac{1}{B_1^3} \iint _\text{unit ball} d^3r d^3 r' \delta ( |\vec{r}- \vec{r}'|-s), ~\qquad  B_1=\frac{4\pi}{3} $$

로 쓰인다. 주어진 단위구 내부의 한 지점 $\vec{r}$에 대해서 적분은 $$S(\vec{r}, s) = \int_\text{unit ball} d^3 r' \delta ( | \vec{r} - \vec{r}' | -s )$$

는 $\vec{r}$에서 반지름 $s$인 구면이 단위구에 포함된 면적을 나타낸다. 그리고 이 값은 $\vec{r}$의 방향에 무관하게 단위구 중심에서 거리에만 의존함을 쉽게 알 수 있다, 즉 

$$ S(\vec{r}, s)= S(r, s)$$

이다. 따라서 $r + s$가 1보다 작을 때와 클 때 두 경우를 별도로 고려해야 한다. 작은 경우는 반지름 $s$인 구면이 완전히 단위구 내부에 포함되므로 

$$ r+s  < 1~~~~~~S(r, s) = 4\pi s^2$$

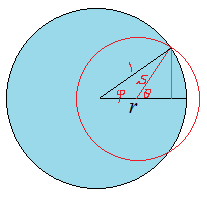
이고, 큰 경우는 (단위원의 경우 그림을 참조하면: https://kipl.tistory.com/732) $4\pi s^2$에서 단위구 밖으로 나가는 구면캡(spherical cap)의 면적을 제외하면 된다. 구면캡의 경도각 범위가 $\cos \theta = \frac{1- r^2 - s^2}{2rs}$이므로 구면캡의 입체각은 

$$ \Delta\Omega = 2\pi \int_0^\theta \sin \theta d \theta  =  2\pi \left(1-\frac{1- r^2 - s^2}{2rs }\right) = 2\pi \frac{(r+s)^2 - 1}{2rs}$$

$$\to~~~ r+ s>1~~~~~~~S(r,s) = (4\pi -\Delta\Omega)s^2 = 4\pi s^2  \frac{1-(r-s)^2 }{4rs}$$

따라서 사이거리에 대한 확률밀도함수는

$$P(s) = \frac{1 }{ B_1^2} 4\pi \int _0^1 r^2 dr S(r,s) $$

$$ = \frac{1}{B_1^2} 4\pi \int_0^{1-s}  r^2 dr ( 4\pi s^2) +  \frac{1}{B_1^2} 4\pi \int_{1-s}^1 r^2 dr   \left(  4\pi s^2 \frac{1- (r-s)^2}{4rs} \right)$$

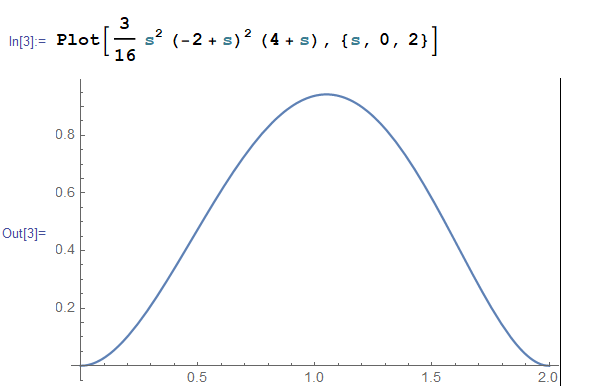
$$ = \frac{3}{16} s^2 (2-s)^2  (4+s) $$

거리의 평균:

$$ <s> = \int_0^2 P(s)sds = \frac{36}{35}$$

거리제곱의 평균:

$$<s^2> = \int_0^2 P(s) s^2 = \frac{6}{5}$$

거리역수의 평균:

$$<\frac{1}{s}>= \int_0^2 P(s) \frac{1}{s} ds = \frac{6}{5}$$

단위원에서 선택한 임의의 두 지점의 사이거리 $s$가 $0\le s\le 2$이 확률밀도함수는 

$$ P(s) =\frac{1}{D_1^2}\iint _\text{unit disk} d^2r d^2 r' \delta (|\vec{r} - \vec{r}'|-s) ,~~~~D_1 = \pi $$

먼저

$$ L(\vec{r}, s) = \int_\text{unit disk} d^2r' \delta (|\vec{r}'-\vec{r}|-s) $$

은 델타함수 제한조건 때문에 $\vec{r}$을 중심으로 한 반지름 $s$인 원과 단위원의 겹치는 영역의 경계의 길이를 의미함을 알 수 있다. 이 $L(\vec{r},s)$가 구해지면 $P(s)$는 이 값을 단위원에 대해 적분을 하면 되는데, 그 값은 단위원의 중심엣 $\vec{r}$가 거리에만 의존함을 쉽게 알 수 있다. 따라서 $\vec{r}$가, 예를 들면  $x$축 위에 있는 경우만 고려하면 충분하다. 또, $L(\vec{r},s) = L(|\vec{r}|=r, s)$이므로

$$\int_\text{unit disk} d^2r L(r,s ) = 2\pi \int_0^1 r dr L(r, s)$$

이제 $\vec{x}$을 중심으로 한 반지름 $s$인 원이 완전히 단위원에 포함이 되는 경우는 원과 단위원의 겹치는 영역이 반지름 $s$인 원이므로 

$$  r + s < 1~~\to ~~~L(r, s)=  2\pi s$$

이고, 원호 일부가 단위원 밖으로 나가는 경우는 두 가지 경우(그림의 $\theta$가 예각 또는 둔각)를 생각할 수 있는데,

두 경우 모두 단위원과 겹치는 영역의 원호의 길이는 그림에서 $2(\pi - \theta)s$인데, $$\sin \varphi = s \sin \theta,~~~~\cos \varphi - s \cos \theta = r$$

$$\to~~~ \cos \theta = \frac{1-r^2 -s^2 }{2rs}$$

$$ r+s>1~~\to~~ L(r, s) = 2(\pi - \theta)s =  2s\left( \pi - \cos ^{-1} \frac{1- r^2 - s^2 }{2rs}\right) $$

로 표현된다. 따라서 사이거리에 대한 확률밀돟함수는

$$P(s) = \frac{2\pi}{\pi^2} \int_0^1 rdr L(r, s) $$$$= 4s \int_0^{1-s} r dr + \frac{4s}{\pi} \int_{1-s}^1 rdr \left( \pi - \cos^{-1} \frac{1- r^2 - s^2 }{2rs} \right)$$

$$=\frac{4s}{\pi} \cos^{-1} \frac{s}{2} - \frac{2s^2}{\pi} \sqrt{ 1 -\frac{s^2}{4}} $$

이 분포를 이용하면 단위원 내부에서 선택된 두 점간의 평균거리는

$$  \left< |\vec{r}-\vec{r}'| \right>= \int_0^2 P(s)s ds = \frac{128}{45\pi} = 0.9054$$

$$  \left< |\vec{r}-\vec{r}'|^2 \right>= \int_0^2 P(s)s^2 ds = 1$$

$$  \left< \frac{1}{|\vec{r}-\vec{r}'|} \right>= \int_0^2 P(s)\frac{1}{s} ds = \frac{16}{3\pi}$$

단위구 내의 두 지점을 $\vec{r}_1$, $\vec{r}_2$라면 두 지점이 선택될 확률이 

$$ P(\vec{r}_1, \vec{r}_2) = \frac{dr_1^3}{B_1}\times \frac{dr_2^3}{B_1}, ~~~~B_1=\text{volume of unit ball} = \frac{4\pi}{3}$$이므로 두 지점의 사이거리의 평균은

$$ \left< |\vec{r}_1 - \vec{r}_2| \right> =\frac{1}{B_1^2} \iint_\text{unit ball} |\vec{r}_1 - \vec{r}_2|   {dr_1^3 dr_2^3} $$

$ \vec{r}_1$과 $\vec{r_2}$의 사이각이 $\theta$일 때 고정된 $\vec{r}_1$에 대해서 $\vec{r}_2$의 극좌표 고도각으로 선택하면 $r_2$에 대한 적분은

$$ I_2 = \int_\text{unit ball} | \vec{r}_1 - \vec{r}_2| dr_2^3$$

$$= 2\pi \int_{0}^1 r_2^2 dr_2 \int_{-1}^1 d \cos \theta \sqrt{r_1^2 + r_2^2 - 2r_1 r_2 \cos \theta }  $$

$$= \frac{2\pi}{3} \int_0^{1} r_2^2 dr_2 \frac{(r_1 + r_2)^3 -| r_1 - r_2|^3 }{r_1 r_2 } $$

$$= \pi \left(1 + \frac{2}{3} r_1^2 - \frac{r_1^4}{15}\right)$$

따라서 사이거리의 평균은

$$ \left< |\vec{r}_1 - \vec{r}_2|\right>= \frac{4 \pi}{B_1^2 } \int_0^1 r_1^2 dr_1 \pi \left(1 + \frac{2}{3} r_1^2 - \frac{r_1^4}{15}\right)$$

$$ = \frac{1}{B_1^2} \frac{64 \pi^2}{ 35} = \frac{36}{35}$$

이전 포스팅에서 거리 역수의 평균이 $\frac{6}{5}$임을 보였는데, 평균거리가 이 값의 역수로 주어지지는 않는 점이 의외다.

아래 그림은 거리에 대한 확률밀도함수를 Monte Carlo 시뮬레이션으로 구한 결과이다. 실제로 거리에 따른 확률밀도함수를 임의의 차원에서 구할 수 있는데, 3차원의 단위구는(ref: J. Math. Phys., Vol. 41, No. 4, April 2000, https://kipl.tistory.com/733)

$$ P_3(s) = \frac{3}{16} s^2 (2-s)^2(4+s),~~~~0\le s\le 2$$

로 계산이 된다. 이 확률밀도함수의 최대값은 $s=1$이 아니라 $s=\frac{1}{5}\sqrt{105}-1=1.04939$ 에서 나온다. $P_3(s)$를 이용하면$$ <s>= \int_0^2 P_3(s) s ds = \frac{36}{35}$$를 얻고, 거리의 역수의 평균은$$ <\frac{1}{s}> = \int_0^2 P_3(s) \frac{1}{s} ds = \frac{6}{5}$$도 얻을 수 있다. 

#define TWO_PI 6.28318530717958647692
// picking a random vector inside an unit ball;
void randomVector(double &x, double &y, double &z) {
    double a = double(rand()) / RAND_MAX;		//[0,1] = radius;
    double b = double(rand()) / RAND_MAX * 2 - 1; //[-1,1] = cos(theta);
    double c = double(rand()) / RAND_MAX * TWO_PI; //[0, 2PI] = azimuthal; 
    a = pow(a, 1.0 / 3.0);
    x = a * sqrt(1 - b * b) * cos(c);
    y = a * sqrt(1 - b * b) * sin(c);
    z = a * b;
}
// Calculate the distance between two randowm points selected 
// inside an unit ball;
double randomDistance() {
    double x1, y1, z1, x2, y2, z2;
    randomVector(x1, y1, z1);
    randomVector(x2, y2, z2);
    x1 -= x2;
    y1 -= y2;
    z1 -= z2;
    return sqrt(x1 * x1 + y1 * y1 + z1 * z1);
}
void meanDistSphere(CRaster& raster) {
    double R = 100;
    int trials = 5000000;
    srand(unsigned(time(NULL)));
    std::vector<int> hist(2 * int(R + .5) + 1, 0);
    for (int i = trials; i-->0;) {
        double d = R * randomDistance();
        hist[int(d)]++;
    }
    double s = 0, sx = 0, sxx = 0;
    double maxh = 0;
    for (int i = hist.size(); i--> 0; ) {
        double h = hist[i];
        maxh = max(h, maxh);
        s += h;
        sx += h * i;
        sxx += h * i * i;
    }
    double mean = sx / s;
    double var = (sxx - sx / s) / s;
    double sdev = sqrt(var);
    // CRaster raster;
    raster.SetDimensions(hist.size(), hist.size(), 24);
    CSize sz = raster.GetSize();
    memset(raster.GetDataPtr(), 0xFF, raster.GetDataSize());
    for (int x = sz.cx; x--> 0; ) {
        int h = int(double(sz.cy) * hist[x] / maxh);
        for (int y = h; y--> 0; ) 
            raster.SetPixel(x, sz.cy-1-y, 0);
    }
    // SaveRaster(raster, "hist.bmp");
}