Geometry & Recognition

$$I = \int_{-1}^{1} \frac{\log (a+x)dx}{x \sqrt{1-x^2}} =   \pi \arcsin \left( \frac{1}{a}\right) \qquad a>1$$

$x= \cos \theta $로 치환을 하면

$$ I = \int_0^\pi \frac{\log(a + \cos \theta) d \theta }{\cos \theta} = \frac{1}{2} \int_0^{2\pi} \frac{ \log( a+ \cos \theta) }{\cos \theta }$$를 얻고, $z= e^{i \theta}$로 다시 치환을 하면

$$ I = \frac{1}{i} \oint _\text{unit circle} \frac{ \log(z^2 + 2a z + 1) - \log(2z)}{1+z^2}$$

따라서 $I$를 구하는 문제는  $$ f(z)= \frac{ \log(z^2 + 2a z + 1) - \log(2z)}{1+z^2}$$의 단위원 위에서 경로적분으로 환원이 된다. $\log$함수 때문에 $z= -a \pm \sqrt{a^1-1}, ~0$이 branch point에 해당하므로 그림의 cutline을 선택한다.

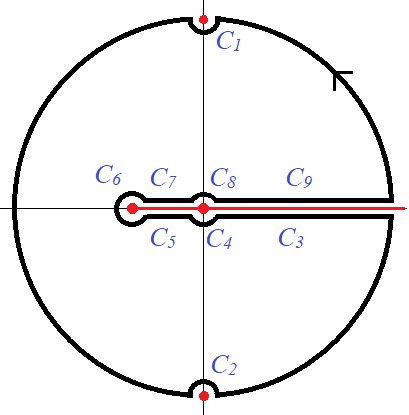
그리고 $z= \pm i$는 $f(z)$의 simple poles에 해당하고, residue는 각각

$$\text{Res}f(\pm i)  =  \frac{\log (a) + i \pi/2}{\pm 2i}~\to ~ \text{Res}f(i) + \text{Res} f(-i) = 0$$

임을 확인할 수 있다.  따라서

$$ \int_{C_1 +C_2} = \pi i \times  \left(\text{Res}f(i) + \text{Res}f(-i)\right)  =0$$

또 $z=0$, $z= -a+\sqrt{a^2-1}$을 감싸는 미소원에서 적분은 0에 수렴함도 확인 할 수 있다.

$$ \int_{C_6+C_4 + C_8} = 0$$

$C_3$과 $C_9$에서는 분모의 두 $\log$함수의 위상이 상쇄되므로 0에 수렴함도 알 수 있다. 마지막으로 $C_5$와 $C_7$는 $\log(2z)$의 cutline에 해당하지 않으므로 적분기여가 없어서,

$$ \int_{C_5 +C_7} = -2\pi i \int_0^{ a-\sqrt{a^2-1}} \frac{dx}{x^2 + 1} $$

$$= - 2\pi i \times \arctan \left( a - \sqrt{ a^2-1}\right) $$

$$= - \pi i \times \arcsin \left( \frac{1}{a}\right)  $$

따라서

$$ \int_{-1}^1 \frac{ \log(a+x) dx}{x \sqrt{1-x^2} } =  \pi \arcsin \left( \frac{1}{a}\right) $$

$$ I = \int_{0}^{2\pi} \frac{d \theta }{1+ \sin^2 \theta} = \sqrt{2} \pi$$

이 적분을 복소함수 적분을 이용하여 구하기 위해서 먼저

$$\sin \theta = \frac{e^{i \theta} - e^{- i \theta}}{2i} \\ \frac{1}{1+\sin ^2 \theta} = \frac{1}{1+ \left( \frac{e^{ i \theta} - e^{-i \theta}}{2i} \right)^2} = \frac{- 4 e^{2i \theta}} { e^{4i \theta}- 6e ^{2i \theta} +1} $$임을 이용하자. 이제 $z= e^{2 i \theta}$로 치환하면 $\theta$에 대한 적분은 복소평면에서 단위원에서 선적분으로 바뀌는데 $\theta:0\to 2\pi$이므로 $z$는 단위원을 따라  두번 감게된다.  따라서 적분은 단위원에서 선적분의 두배가 되어야 한다.

그리고

$$ dz = 2i e^{2 i \theta} d \theta \\ I = 2\times \oint_\text{unit circle} \frac{2i  dz}{z^2 - 6z + 1}$$

$z= 3 \pm2\sqrt{2}$가 simple poles인데, 이 중 $z_1 = 3-2\sqrt{2}$가 단위원에 포함이 된다. $z_1$에서 residue는 $$ \text{Res} f(z_1) = \frac{2i }{z_1 - z_2 } = \frac{2i}{- 4\sqrt{2}} $$ 이므로 residue 정리에 의해서 $$ I = 2 \times \left( 2\pi i \times \frac{2i }{-4 \sqrt{2}}\right) = \sqrt{2} \pi$$ 동일한 방법으로 다음 결과를 얻을 수 있다.

$$ \int_0^{2\pi} \frac{d \theta}{ 1+ \cos^2 \theta} = \sqrt{2} \pi$$

\begin{gather} \int_{-\pi}^\pi \frac{ \theta \sin \theta d \theta }{a+ \sin \theta}  = \frac{\pi a}{\sqrt{a^2-1}} \left( \pi - \tan ^{-1} \sqrt{a^2-1}\right) \\ \int_{-\pi}^\pi \frac{ \theta \cos \theta d \theta }{a+ \sin \theta} = 2\pi \log \left( 2a^2 -2a \sqrt{ a^2 -1} \right)\end{gather}

함수 $$f(z) =\frac{2z \log z}{z^2 + 2i a z -1},\qquad a>1$$의 경로적분을 고려하자. Brach point가 $z=0$이므로 음의 $x$ 축을 cutline으로 선택한다. 그러면 $-\pi \le \arg(z) \le \pi $. 적분경로는 그림과 같이 반지름 1인 원으로 선택하자.

그러면 simple pole $z_1= -i (a- \sqrt{a^2-1})$은 경로 내부에 포함이 된다. 그리고 residue는 

$$ \text{Res} f(z_1) = -\frac{(a - \sqrt{ a^2-1}) \big[ \log (a- \sqrt{a^2-1} ) -i \pi/2 \big] }{\sqrt{a^2-1}}$$

경로 $C_1$에서 $ z= x e^{-i \pi}~(x:0\to1)$이므로 

$$\int_{C_1} = 2 \int_0^1 \frac{x(\log x - i \pi) dx }{ x^2 - 2iax -1}$$

경로 $C_3$에서 $z= x e^{i\pi}~(x: 1 \to 0)$이므로, 

$$ \int_{C_3} = -2 \int_0^1 \frac{x(\log x + i \pi) dx }{x^2 - 2i ax -1}$$이어서

\begin{gather} \int_{C_1+C_3} = - 4\pi i \int_0^1 \frac{xdx}{x^2 - 2ia x-1} \\  =-4\pi i \int_0^1 \frac{(x^2 -1 + 2ia x)xdx}{(x^2-1) ^2 + 4 a^2 x^2 } \\ = -2\pi i \int_{-1}^0 \frac{u du}{u^2 + 4a^2 u + 4a^2} +8 \pi a \int_{0}^1 \frac{ x^2 dx}{(x^2-1)^2 + 4a^2 x^2 }\\ = -2\pi i \left( \log (2a) + \frac{a\log( a -  \sqrt{a^2-1})  }{\sqrt{a^2-1}}\right)\\  +\frac{2\pi}{\sqrt{a^2-1}} \left(\frac{\pi}{2} \sqrt{a^2-1} - a\tan^{-1} \sqrt{a^2-1} \right)\end{gather}

그리고 $C_2$에서는 $z= e^{i \theta}~(\theta:-\pi \to \pi)$이므로

\begin{gather}\int_{C_2} = 2\int_{-\pi}^\pi  \frac{( i \theta e^{i \theta} ) ( i \theta e^{i \theta} d \theta)}{ e^{2i \theta} + 2i a e^{i \theta} -1} \\= 2\int_{-\pi}^\pi \frac{ i^2  \theta e^{i \theta} d \theta }{e^{i \theta} + 2i a - e^{- i \theta} }\\  =  \int_{-\pi}^\pi \frac{ ( - \theta \sin \theta + i \theta \cos \theta) d \theta }{a + \sin \theta}\end{gather}

그리고 $C_\epsilon$에서 적분은 0에 수렴한다. 정리하면 

\begin{gather} \int_{-\pi}^\pi \frac{ \theta \sin \theta d \theta }{a+ \sin \theta}  = \frac{\pi a}{\sqrt{a^2-1}} \left( \pi - \tan ^{-1} \sqrt{a^2-1}\right) \\ \int_{-\pi}^\pi \frac{ \theta \cos \theta d \theta }{a+ \sin \theta} = 2\pi \log \left( 2a^2 -2a \sqrt{ a^2 -1} \right)\end{gather}