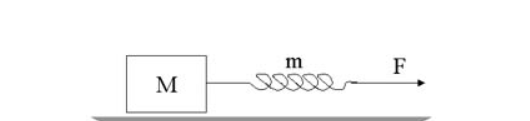
질량 $m$인 무거운 용수철에 연결된 질량 $M$인 물체를 힘 $F$를 주어 당기고 있다. 용수철이 늘어난 길이는? 단, 용수철 상수는 $k$이다.
1. $\frac{2m+M}{2k(m+M)}F$
2. $\frac{m+2M)}{2k(m+M)}F$
3. $\frac{m+M}{k(2m+M)}F$
자연상태(길이 $=L$)의 용수철에 늘렸을 때 왼쪽에서 $x$만큼 떨어진 지점이 $f(x)$만큼으로 늘어난다면 미소부분 $dx$는 $dx +df$의 길이로 된다. 그리고 미소부분의 용수철 상수는 $k L/dx$이다 (용수철은 짧게 만들면 용수철 상수가 커진다).

용수철이 가속도 $a$로 움직인다면 늘어난 미소부분에 걸리는 장력이 왼쪽 부분과 물체 $M$을 가속시키므로
$$ T= k\frac{L}{dx} df = kL \frac{df}{dx} =\Big( \frac{m}{L} x +M \Big)a $$
을 얻는다. 따라서
$$\frac{df}{dx}= \frac{a}{k} \left( \frac{m}{L^2} x + \frac{M}{L} \right) ~\Longrightarrow~f(x) = \frac{a }{2k} \Big(m \Big(\frac{x}{L}\Big)^2 + 2M\frac{x}{L} \Big) $$
물체와 용수철에 작용하는 외력이 $F$이므로
$$a = \frac{F}{m+M} \quad \rightarrow~ \therefore f(L)= \frac{m + 2M}{2k(m+M)} F$$
확인: $m=0$인 경우 늘어난 길이는 $\frac{F}{k}$이어야 한다. 그리고 $m \gg M$인 경우는 $\frac{F}{2k}$이어야 한다.
무거운 용수철을 사용한 진자의 주기는?
용수철의 질량을 무시할 수 없는 경우 용수철 진자의 주기는 질량이 없는 경우보다 1. 길어진다. 2. 짧아진다. 3. 변함없다. 더보기 더보기 용수철에 매달린 물체의 속도가 $v$일 때 용수철이 가지
kipl.tistory.com
'Physics > 역학' 카테고리의 다른 글
| 각도의 시간 의존성은? (0) | 2022.02.26 |
|---|---|
| 설현은 수지를 따라 잡을 수 있을까? (0) | 2022.02.25 |
| 충돌 직후 질량중심의 속도는? (0) | 2022.02.25 |
| 줄을 당기는데 필요한 힘은? (0) | 2022.02.24 |
| 막대에 작용하는 힘은 (0) | 2022.02.24 |




