Geometry & Recognition

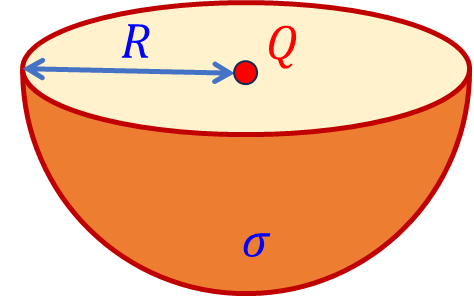
반구면의 미소면적 $\Delta A$에 작용하는 정전기력은 면에 수직하게 $\sigma \Delta A Q/(4\pi \epsilon_0 R^2) $ 만큼 작용한다. 따라서 정전기력이 구면에 만드는 압력은 $P = \sigma Q / (4\pi \epsilon_0 R^2)$이다. 반구면을 미소링으로 분해해서 이 압력이 만드는 알짜힘을 구할 수 있지만 적분을 사용하지 않는 다른 방법을 사용하자. 압력 $P$을 가지는 기체를 적도면이 닫힌 반구면에 가둘 때 압력이 만드는 알짜힘이 0이 되어야 하므로 반구면이 받는 알짜힘은 적도면이 받는 알짜힘과 같음을 알 수 있다. 그런데 압력이 적도면에 주는 힘은 모두 같은 방향이므로 단순하게  $\pi R^2 P= \sigma Q/(4\epsilon_0)$로 계산된다.

내부 한 점 P에서 전기장은 구면의 각 지점의 전하가 기여하는 전기장의 합인데, 그림처럼 대칭적으로 그린 미소 입체각에 해당하는 미소 면적(A와 C, 또는 B와 D)내의 전하가 P점에서 만드는 전기장은 방향은 서로 반대이고 크기는 같기 때문에(P에서 거리가 멀면 그 제곱에 비례해서 면적이 늘어나서 전하가 증가하지만 전기장 세기는 거리의 제곱에 반비례하므로) 상쇄되어 0이 된다(가우스 법칙으로 쉽게 보일 수도 있다). 따라서 적도면에서 같은 각만큼 기울어진 반구상의 같은 미소 입체각을 갖는 두 미소 면적 A와 B의 전하는 각 미소면적에서 P을 향하는 방향으로 방향의 전기장을 만드는데 그 크기는 같음을 알 수 있고, 더하면 적도면 수평성분은 사라져서 수직성분만 남게 된다.