Geometry & Recognition

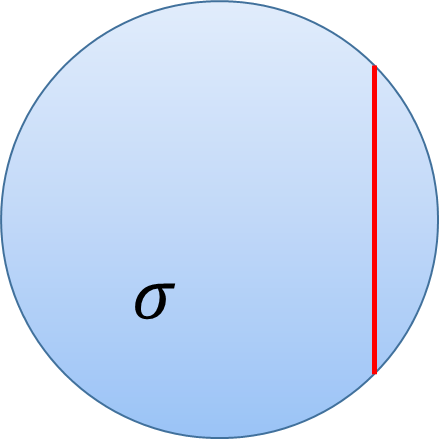
균일한 전하밀도 $\rho>0$을 가지는 전하분포가 있다. 이 분포의 한 지점에서 전기장이 $\vec{E}_c$ 이고, 전위가 $V_c$ 다. 이제 이 지점을 중심으로 구형 영역 내부의 전하를 제거한다. 그러면 이 구형 영역 중심에서의 전기장과 전위는 어떻게 변할까?

• 전기장 세기: 감소한다, 그대로, 커진다.
• 전기장 방향: 변한다, 그래로
• 전위: 감소한다, 그대로, 증가한다.

평행판 축전기가 있다. 두 극판 중심평면상에 있는 외부 한 지점에서 전기장은?

풀이: 

중앙평면에서는 대칭성에 의해서 전기장은  $y$ 성분만 존재한다. 극판전하밀도가 일정할 때,

$$ E_y = - 2 \times \frac{1}{4\pi \epsilon_0 } \int_\text{upper} \frac{\sigma dA \sin \theta }{r^2} $$인데 $dA \sin \theta$는 P에서 본 미소면적 $dA$의 정사영이므로 $dA\sin \theta /r^2 $은 P에서 본 $dA$의 입체각에 해당한다(정사영은 코사인을 쓰는 것이 좀 더 직관적인데 이렇게 하려면 각도를 극판에 수직한 방향에 대해서 정의하면 된다). 따라서

$$ E_y = -\frac{\sigma}{2\pi \epsilon_0 } \Omega$$

로 쓸 수 있다. $\Omega$는 P에서 본 위쪽 극판의 입체각이다. 극판에서 멀리 떨어진 지점일 경우(P에서  두 극판 중심까지 거리가 $R$) 

$$ \Omega \approx  \frac{A\sin \theta_0 }{R^2},~~~~\tan \theta_0 =\frac{d/2}{R}\approx \sin \theta_0$$이므로

$$ E_y \approx - \frac{\sigma A d}{4\pi \epsilon_0 R^3}= -\frac{p}{4\pi\epsilon_0 R^3}$$여기서 극판 전하에 의한 전기쌍극자 모멘트 $p$는 각 극판을 점전하로 본 근사식 $p\approx \sigma A d$을 썻다. 이 결과는 극판에서 먼 지점에서는 두 반대 부호의 극판이 만드는 전기쌍극자에 의한 전기장으로 근사됨을 보여준다.

표면전하밀도 $\sigma$ 균일하게 대전된 구면(반지름 $R$)에 작은 구멍을 만들었다. 잘려진 cap의 중앙 P 지점에서 전기장의 세기는?

풀이: 대칭성에 의해서 전기장의 방향은 OP 방향임을 쉽게 알 수 있다. 이 방향 성분은

$$ E_x = \frac{1}{4\pi \epsilon_0} \int_\text{sphere with a hole} \frac{ \sigma dA  \hat{r} \cdot \hat{x}}{r^2}$$

$$ = \frac{\sigma}{4\pi \epsilon_0} \int_\text{sphere with a hole} d\Omega = \frac{\sigma}{4\pi \epsilon_0} \int_{0} ^{ \pi /2- \theta_0/2} 2\pi \sin \theta d \theta$$

$$ = \frac{\sigma} {4\pi \epsilon_0} 2\pi \left(1- \cos \left(\frac{\pi}{2}- \frac{\theta_0}{2}\right)\right) = \frac{\sigma}{2\epsilon_0} \left( 1-\sin \frac{\theta_0}{2} \right)$$

그리고 구멍의 크기가 매우 작은 경우엔 ($\theta_0 \ll 1$)

$$ E_x \approx \frac{\sigma}{2\epsilon_0}$$로 근사된다. 이 결과는 중첩의 원리를 고려하면 쉽게 이해가 된다. 온전한 구면전하가 표면에 만드는 전기장($E_\text{whole sphere}=\sigma/\epsilon_0$)은 구멍이 있는 구면이 만드는 전기장($E_x$)과 떼어져 나간 작은 조각의 전하가 만드는 전기장($E_\text{patch} = \sigma/2\epsilon_0$)의 합으로 이해하면 구할 수 있다.

중심에 $+q$ 점전하가 고정되어 있는 도체 구각이 있다. 이 구각 주변에 $+Q$의 점전하를 가져다 놓는 경우 내부의 한 지점 $A$에서

[Q1] 전기장은 변하는가 아니면 변하지 않는가?

[Q2] 전위는 변하는가(증가/감소) 아니면 변하지 않는가?

[Q1] 균일한게 대전된 구면이 있다. 구면을 그림처럼 자르면 단면은 원이 된다. 원의 중심에서 왼쪽 부분의 전하가 만드는 전기장의 세기 $E_L$과 오른쪽 부분의 전하가 만드는 전기장의 세기 $E_R$을 비교하면?

1. $E_L > E_R$
2. $E_L = E_R$
3. $E_L < E_R$
4. 정보가 부족

[Q2] 단면원 중심에서 왼쪽 부분 전하에 의한 전위 $V_L$과 오른쪽 부분 전하에 의한 전위 $V_R$을 비교하면?

1. $V_L< V_R$
2. $V_L= V_R$
3. $V_L > V_R$
4. 정보가 부족