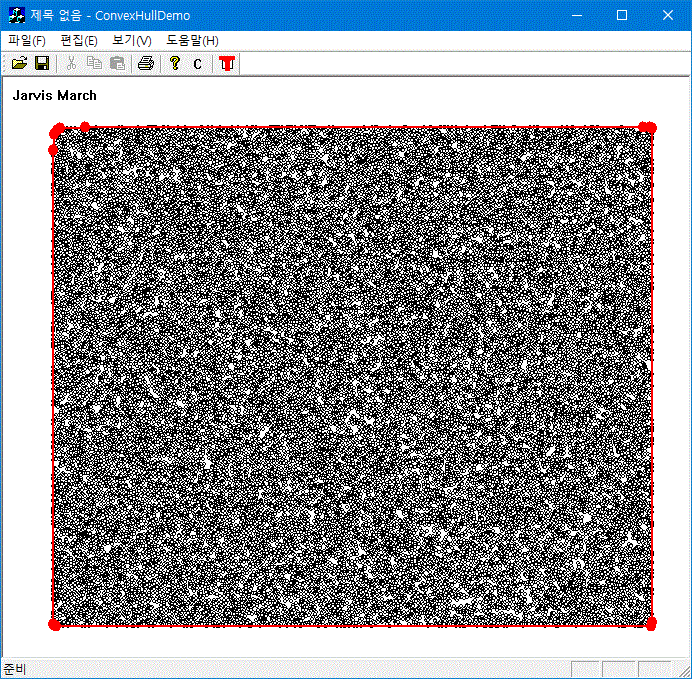
기하 알고리즘에서 입력점의 개수가 많아지면 중복점이 생기고, 이 때문에 최적화에 주안점을 둔 알고리즘은 중복점에 대한 예외처리를 하지 않으면 정상적으로 동작하지 않는 경우가 종종 생긴다. 안정성과 구현의 간결함을 유지하고 싶으면 좀 더 brute force method에 가까운 알고리즘을 사용하는 것도 고려해 볼 수 있다. 다음은 Jarvis March 알고리즘을 써서 2차원 convex hull을 구하는 코드이다. (그림은 50,000개의 입력점을 사용함.)
BOOL ccw(const CPoint &a, const CPoint &b, const CPoint &c){
// cross(ac, ab) < 0: ab가 ac보다 오른쪽에 있음 = b가 ac변의 오른쪽에 있음.
return ((c.x - a.x) * (b.y - a.y) - (c.y - a.y) * (b.x - a.x)) < 0;
}
std::vector<CPoint> JarvisMarch(const std::vector<CPoint> &pts) {
int n = pts.size();
if (n < 3) return std::vector<CPoint> (); //null_vector;
int left = 0;
for (int i = 1; i < n; i++) //convex hull의 첫번째는 맨 왼쪽 점;
if (pts[i].x < pts[left].x) left = i;
int turns = 0; //debug 용도
int prev = left;
std::vector<CPoint> hull;
while (1) {
hull.push_back(pts[prev]);
int next = (prev + 1) % n;
// prev-next 변이 모든 점의 오른쪽에 있게 하는 next를 찾으면 됨;
// 없으면 next가 convex hull 위의 점임;
for (int i = 0; i < n; i++) {
if (i == next || i == prev) continue;
if (ccw(pts[prev], pts[i], pts[next]))
next = i;
}
prev = next;
turns++; //debug 용도;
if (prev == left) break;
}
TRACE("number of turns = %d\n", turns);
remove_collinear(hull); // removes collinear vertices(optional);
return hull;
}더보기
int remove_collinear(std::vector<CPoint>& V) {
int N = V.size();
if (N < 3) return 0;
// 먼저, 일직선상에 있지 않는 vertex을 찾음;
int start;
for (start = 0; start < N; start++)
if (ccw(V[(start - 1 + N) % N], V[start], V[(start + 1) % N]))
break;
std::vector<CPoint> H;
H.push_back(V[start]);
int prev = start;
int curr = (prev + 1) % N;
int next = (curr + 1) % N;
while (curr != start) {
if (ccw(V[prev], V[curr], V[next])) {
H.push_back(V[curr]);
prev = curr;
}
curr = (curr + 1) % N;
next = (curr + 1) % N;
}
std::swap(V, H);
return V.size();
};728x90
'Computational Geometry' 카테고리의 다른 글
| Convex Hull Peeling (0) | 2021.03.29 |
|---|---|
| Graham Scan (0) | 2021.03.28 |
| Approximate Minimum Enclosing Circle (1) | 2021.03.18 |
| Minimum Bounding Rectangle (3) | 2021.03.15 |
| Minimum Enclosing Circle (0) | 2021.03.01 |




