지상에서 포물선 운동을 하는 물체의 속도 벡터를 모두 모아 시작을 같게 만들면 속도 벡터의 끝이 그리는 자취(hodograph라 함)는 직선이 된다. 이는 속도의 차이가 가속도이고 지상에서 중력가속도는 크기와 방향이 일정하기 때문이다.
$$\vec {v}(t) =\vec {v}_0 - g\hat {j} t$$
태양계에서 행성은 태양을 한 초점으로 하는 타원 궤도상에서 움직인다. 그러면 행성의 각 지점에서 속도 벡터의 시작점을 한 지점에 모을 때 벡터의 끝점이 그리는 궤적은 무엇일까? 원 궤도를 그리면 속력이 일정하므로 당연히 원이 될 것으로 예상할 수 있지만, 타원 궤도에서는 속력은 에너지 보존을 고려하면 일정할 수 없다. 그런데 타원궤도를 그리는 경우에도 속도의 hodograph는 원궤도에서와 마찬가지로 벡터 공간에서 원으로 표현된다. 왜 그럴까?
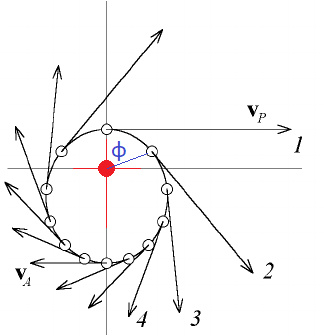
행성이 받는 중력은 태양으로부터 거리의 제곱에 반비례하므로 운동방정식을 사용하면 속도의 변화량의 크기는
$$ \frac {d\vec {v}}{dt}= -\frac {GM}{r^2 }\hat {r} \quad \rightarrow\quad |\Delta \vec {v}| =\frac {GM}{r^2} \Delta t$$
임을 얻을 수 있다. 또한 태양의 중력이 중심력이므로 각운동량 보존(또는 Kepler의 제 2법칙)된다는 사실에서 마찬가지로 속도 변화량의 크기에 대한 식(각도 $\varphi$는 태양을 원점으로 하여 측정한다)
$$ L =m |\vec{r}\times \vec {v}| = m r^2 \frac {d\varphi}{dt} \quad\rightarrow\quad \Delta\varphi =\frac {L}{mr^2}\Delta t$$을 얻을 수 있다. 두 식에서 $\Delta t / r^2$을 소거하면,
$$ |\Delta \vec{v}| = \frac {GMm}{L} \Delta \varphi$$이고, 각운동량 크기가 일정하므로 속도의 증가량의 크기가 회전각의 증가에 비례함을 보여준다. 이는 태양을 중심으로 행성 궤도를 일정한 각크기로 나눌 때 각 인접 지점과의 속도차의 크기가 항상 일정함을 의미한다. 기하학적으로는 일정한 각도차가 있는 궤도상의 각 지점에서 속도 벡터를 가져와서 시작을 (벡터 공간의) 한 지점에 모으면 벡터의 머리가 일정하게 변함을 의미하고, 이는 벡터의 머리가 반지름이 일정한($GMm/L$)인 원주상에 있을 때만 가능한 관계이다. (주의: 벡터 공간에서 벡터의 시작점이 각을 재는 원점이 아니다. 왜냐하면 원과 달리 타원에서는 위치와 속도 벡터는 서로 직교하지 않는다.) hodograph의 반지름은 근일점에서 속력 $v_P$와 원일점에서 속력 $v_A$의 절반임으로 표현되는데 $v_R = (v_A + v_P)/2 = \frac {GMm}{L}$임을 근일점, 원일점에서 역학적 에너지 보존과 각운동량 보존식을 이용해서 확인할 수 있다.
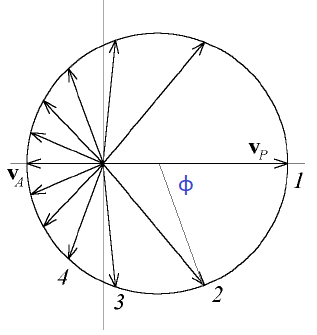
설명 동영상:
'Physics > 역학' 카테고리의 다른 글
| 불타는 양초 시소 (3) | 2021.01.17 |
|---|---|
| 용수철 저울의 눈금은? (0) | 2021.01.17 |
| 태양계의 행성 운동에서 각운동량 보존법칙 (0) | 2021.01.15 |
| 사람은 얼마나 빨리 걸을 수 있을까? (0) | 2021.01.14 |
| 연필이 넘어져서 바닥에 닿는데 걸리는 시간은? (0) | 2021.01.09 |




