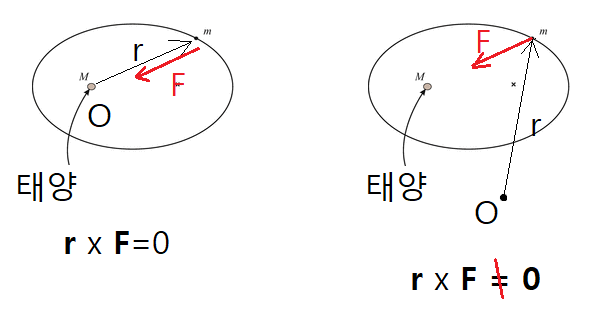
태양계의 행성 운동에서 각운동량 보존법칙

태양계의 행성 운동에서 각운동량은 보존이 된다(Kepler의 제2법칙). 이는 태양이 행성에 작용하는 힘인 만유인력이 중심력의 형태를 띠고 있기 때문이다. 식으로는 태양에서 행성까지 위치 벡터를 $\vec {r}$이라면 태양이 행성에 작용하는 만유인력은 $\vec {F} = \frac {GMm}{r^3}\vec {r}$로 쓸 수 있으므로 만유인력이 만드는 토크가 $\vec {\tau} = \vec {r}\times \vec {F}=0$임을 쉽게 알 수 있다. 따라서 각운동량 보존은 자명해진다.

만약 행성의 위치를 재는 원점을 태양이 아니라 다른 지점으로 잡으면 어떻게 될까? 이 경우 만유인력의 방향과 위치 벡터의 방향이 나란하지 않으므로 토크가 0이 안된다. 그럼 각운동량은 원점을 어디로 잡는가에 따라 보존되기도 하고 안되기도 하는 물리량일까? 무엇을 놓치고 있는 것일까?