$$f(t) = {\cal L}^{-1} \left[ \frac{1}{s}\exp\left( -\frac{s}{\sqrt{1+s^2}}\right) \right](t)$$
역 Laplace 변환을 Bromwich 적분으로 표현하면 $$f(t) = \frac{1}{2\pi i}\int_{\gamma-i\infty}^{\gamma +i\infty} F(s) e^{st}ds=\frac{1}{2\pi i} \int_{C} \frac{1}{z}\exp \left(- \frac{z}{\sqrt{1+z^2}} +z t \right) dz$$ 적분경로 $C= \{C_1+C_2+C_3+C_4+C_\epsilon + \text{half circle}\}$는 그림의 폐경로에서 오른쪽 $z=\gamma$ 을 통과하는 수직선을 제외한 나머지 부분이다. 제곱근 함수 때문에 branch cut을 $z=\pm i$을 연결하는 선분으로 잡는다. 이 경우 위상은 $$ -\frac{\pi}{2} \le \arg(z-i) , ~\arg(z+i) \le \frac{3\pi}{2}$$ 로 잡을 수 있다.
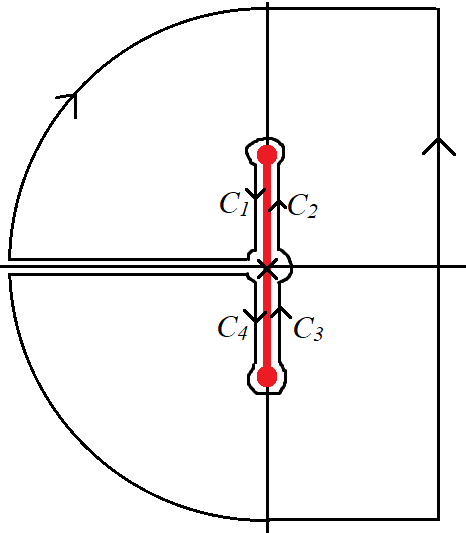
그러면 각 경로에서,
$$ C_1:~~z=y e^{i\pi/2}, ~ z-i=(1-y) e^{i 3\pi/2}, ~z+i= (1+y)e^{i\pi/2},~y:1\to0$$
$$ C_2:~~z=y e^{i\pi/2}, ~ z-i=(1+y) e^{ - i \pi/2},~z+i = (1-y)e^{i\pi/2},~y: 0\to1$$
$$ C_3:~~z=y e^{-i\pi/2}, ~ z-i=(1+y) e^{-i \pi/2},~z+i = (1-y)e^{i\pi/2},~y:0\to1$$
$$ C_4:~~z=y e^{-i\pi/2}, ~ z-i=(1-y) e^{i 3\pi/2},~z+i = (1+y)e^{i\pi/2},~y:1\to0$$
따라서
$$ \int_{C_1} = \int_1^0 \exp\left( \frac{iy}{\sqrt{1-y^2} } + iyt\right) \frac{dy}{y}$$
$$ \int_{C_2} = \int_0^1 \exp\left( \frac{-iy}{\sqrt{1-y^2} } + iyt\right) \frac{dy}{y}$$
$$ \int_{C_3} = \int_1^0 \exp\left( \frac{iy}{\sqrt{1-y^2} } - iyt\right) \frac{dy}{y}$$
$$ \int_{C_4} = \int_0^1 \exp\left( \frac{-iy}{\sqrt{1-y^2} } - iyt\right) \frac{dy}{y}$$
그리고 simple pole $z=0$을 감싸는 적분은 ($z=\epsilon e^{i \theta}$)
$$ \int_{C_\epsilon} = 2\pi i $$
이므로 $f(t)$는 다음과 같이 쓸 수 있다.
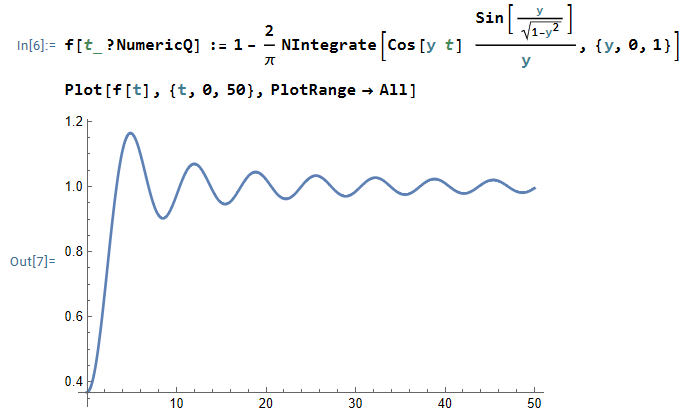
$$ f(t) = 1 -\frac{2}{\pi} \int_0^1 \cos (yt) \sin \left( \frac{y}{\sqrt{1-y^2}} \right) \frac{dy}{y}$$
'Mathematics' 카테고리의 다른 글
| Inverse Laplace Transform을 이용한 열방정식 해 (1) | 2024.10.23 |
|---|---|
| Inverse Laplace Transform as Bromwich Integral-4 (0) | 2024.10.22 |
| Inverse Laplace Transform as Bromwich Integral-2 (3) | 2024.10.20 |
| Integration along a branch cut-028 (0) | 2024.10.19 |
| Integration along a branch cut-027 (0) | 2024.10.15 |




