$$ f(t)= {\cal L}^{-1} \left[ \frac{1}{s(s-1)} \exp\left(-\sqrt{\frac{s-1}{s}} \right)\right](t)$$
그림과 같은 경로에서 $\oint F(z) e^{zt} dz = 0$이므로
$$f(t) =\frac{1}{2\pi i} \int_{\gamma-i \infty}^{\gamma +i \infty} F(s) e^{st} ds = - \frac{1}{2\pi i} \int_{C} \frac{e^{zt}}{z(z-1)} \exp\left(-\sqrt{\frac{z-1}{z}} \right) dz$$
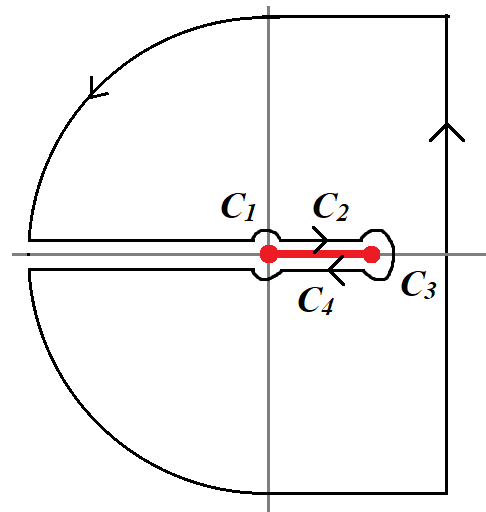
$$ -\pi \le \arg(z), \arg(z-1) \le \pi$$
$C_1$에서 $z=\epsilon e^{i \theta}$이므로
$$\int_{C_1} = 0$$
$C_3$에서 $z= 1+ \epsilon e^{i \theta} ~(\theta: \pi \to -\pi)$,
$$\int_{C_3} \frac{ e^{zt}}{z(z-1)} \exp\left( -\sqrt{\frac{z-1}{z}}\right) dz = -2\pi i e^{t} $$
$C_2$에서 $z=x e^{i 0}$, $z-1= (1-x) e^{i \pi}~(x:0\to 1)$이므로
$$ \int_{C_2} = \int_0^1 \frac{e^{xt} }{x(x-1)} \exp\left( - i\sqrt{\frac{1-x}{x}} \right) dx$$
$C_4$에서 $z=x e^{i 0}$, $z-1=(1-x) e^{-i \pi}~(x:1\to0)$이므로
$$\int_{C_4} =\int_1^0 \frac{ e^{xt}} { x(x-1)} \exp\left( i\sqrt{\frac{1-x}{x}} \right) dx$$
따라서 정리하면
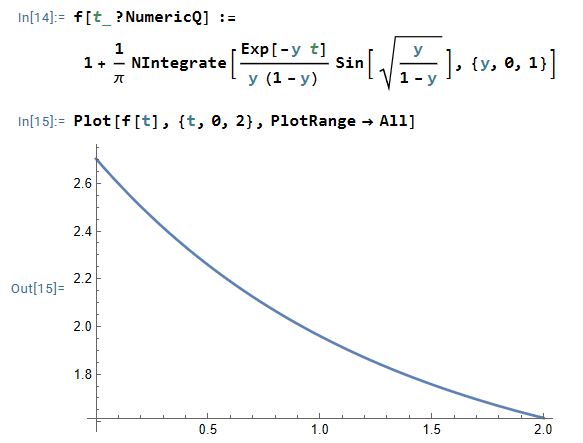
$$f(t) = e^{t} + \frac{1}{\pi} \int_0^1 \frac{e^{xt}}{x(x-1)} \sin \left( \sqrt{\frac{1-x}{x}} \right) dx \\ = e^t\left[ 1+ \frac{1}{\pi} \int_0^1\frac{e^{-yt}}{y(1-y)}\sin \left( \sqrt{\frac{y}{1-y}} \right)dy \right]$$
'Mathematics' 카테고리의 다른 글
| Inverse Laplace Transform을 이용한 무한 LC Ladder Circuit에서 Step Respose (0) | 2024.10.24 |
|---|---|
| Inverse Laplace Transform을 이용한 열방정식 해 (1) | 2024.10.23 |
| Inverse Laplace Transform as Bromwich Integral-3 (0) | 2024.10.20 |
| Inverse Laplace Transform as Bromwich Integral-2 (3) | 2024.10.20 |
| Integration along a branch cut-028 (0) | 2024.10.19 |



