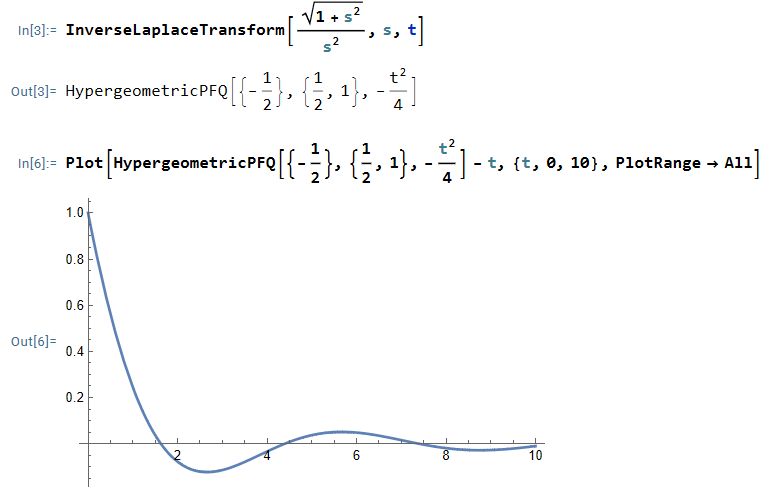
$$ f(t) = {\cal L }^{-1} \left[\frac{ \sqrt{ s^2 + 1}}{s^2} \right](t)$$
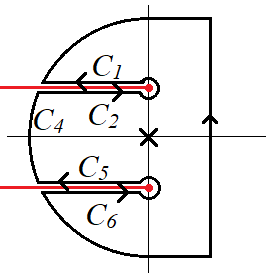
Inverse Laplace 변환을 Bromwich 적분으로 표현하기 위해 그림과 같은 폐경로를 고려하면 ($C=\sum C_i$) $$ \oint_\Gamma F(z) e^{sz} dz = \left( \int _{\gamma - i\infty}^{\gamma + i\infty} - \int_C \right) F(z) e^{sz} dz = 2\pi i \times \text{Res} (z=0)$$인데, $z=0$이 double pole이므로, $$ f(t) = \left.\frac{d}{dz} \left(e^{tz} \sqrt{ z^2 + 1}\right) \right|_{z=0} +\frac{1}{2\pi i} \int_{C} \frac{\sqrt{z^2 + 1} }{z^2} e^{tz}dz$$ Branch cut을 $z= \pm i$을 연결하는 선분 대신 그림과 같이 각각 $z=\pm i$에서 출발하는 두 개의 반직선으로 선택한다: $-\pi \le \arg(z-i), ~\arg(z+i)\le \pi$
경로 $C_1$에서 $$z=-x + i, ~z-i = x e^{i\pi},~z+i = \sqrt{x^2 + 4} e^{i \theta}$$
여기서 $\tan\theta = -x/2$, $x: 0 \to \infty$이다.

$\cos \theta = -x/ \sqrt{x^2 + 4}$임을 이용하면
$$ \sqrt{z^2 +1} = \sqrt{(z-i)(z+i)} = \sqrt{x} \sqrt[4]{x^2+4} e^{i\pi/2}e^{ i\theta/2}\\ = i \sqrt{x} \sqrt[4]{x^2+4} \left(\cos \frac{\theta}{2}+ i\sin \frac{\theta}{2} \right) \\=i \sqrt{x} \left[ \sqrt{\sqrt{x^2/4+1}-x/2}+i \sqrt{\sqrt{x^2/4+1}+ x/2}\right] \\ \equiv i \sqrt{x}(g_1 + ig_2) $$
그리고 $C_2$에서는 $z-i = x e^{-i \pi}$이므로 (note: $z^2 = x^2 -1 -2ix$)
$$ \int_{C_1} = \int _{C_2} = - \int_{0}^\infty i \sqrt{x} \frac{ g_1 + i g_2}{x^2-1 - 2i x} e^{-xt} e^{i t} dx$$
마찬가지로 $C_5, C_6$에 대한 적분도 ($z\to -x-i$, $\theta\to - \theta$)
$$ \int_{C_5} = \int_{C_6} = -\int_0^\infty i \sqrt{x} \frac{g_1 -i g_2}{x^2 - 1 + 2ix}dx e^{-xt} e^{-it} dx$$
이므로
$$ f(t) = t - \frac{2}{\pi} \int_0^\infty dx \sqrt{x} e^{-xt} \frac{(x^2-1) (g_1 \cos t-g_2\sin t)- 2x ( g_1 \sin t + g_2\cos t)}{(x^2 +1)^2 }$$

'Mathematics' 카테고리의 다른 글
| Inverse Laplace Transform as Bromwich Integral-4 (0) | 2024.10.22 |
|---|---|
| Inverse Laplace Transform as Bromwich Integral-3 (0) | 2024.10.20 |
| Integration along a branch cut-028 (0) | 2024.10.19 |
| Integration along a branch cut-027 (0) | 2024.10.15 |
| Integration along a branch cut-026 (0) | 2024.10.14 |



