보통 베르누이 방정식은 에너지 보존을 써서 유도한다. 에너지 보존식이 뉴턴의 운동방정식에서 나온 결과이므로 베르누이 방정식 또한 운동방정식에서 직접 유도할 수 있다(steady, incompressible, frictionless flow). 유체 입자가 움직이는 경로인 유선 상의 한 지점을 고려하자. 이 지점에서 가속도 벡터는 유선의 접선 방향과 그 지점에서 곡률 중심을 가리키는 법선 방향 성분으로 분해가 가능하다. 유선은 유선의 길이 ($s$)를 매개변수로 써서 표현할 수 있으므로 이를 이용하면 가속도의 접선 성분은
$$ a_t = \frac{d |\vec{v}|}{dt}= \frac{dv}{dt} = \frac{dv}{ds}\frac{ds}{dt} = \frac{dv}{ds}{v} = \frac{1}{2} \frac{dv^2}{ds}$$
가속도의 법선 성분은 구심가속도이므로 그 지점에서 곡률 반지름이 $R$이면
$$ a_n = \frac{v^2}{R}$$
유선상의 한 지점을 중심으로 하는 부피가 $dV = ds dA$인 미소 박스를 생각하자.
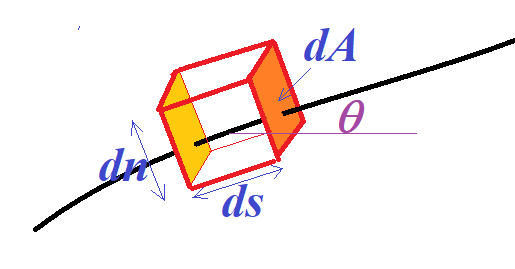
이 미소 박스에 작용하는 접선 방향의 알짜힘은 박스 좌우에서 작용하는 압력의 차이가 만드는 힘과 중력의 접선성분의 합으로 주어진다:
\begin{align}\sum F_t &= - P(s+ds/2) dA + P(s-ds/2) dA - \rho g \sin \theta dV \\ &= -\Big( \frac{dP}{ds} + \rho g \sin \theta \Big) dV \end{align}
미소 부피 속의 유체 질량이 $dm = \rho dV$이므로 접선 방향의 운동방정식은
$$ -\frac{dP}{ds} -\rho g \sin \theta = \frac{1}{2} \rho \frac{dv^2}{ds} $$
그런데 유체는 비압축성이고, $\sin \theta = dz/ds$이므로 다음과 같이 베르누이 방정식을 얻을 수 있다:
\begin{gather}\frac{d}{ds}\Big( P + \frac{1}{2} \rho v^2 + \rho g z \Big) = 0 \\ \text{or}\quad P +\frac{1}{2}\rho v^2 + \rho g z = \text{const} \end{gather}
법선 방향의 운동방정식도 같은 방법으로 유도할 수 있는데, 법선 방향의 압력 변화를 $dP/dn$이라면
$$\frac{dP}{dn} + \rho \frac{v^2}{R} + \rho g \frac{dz}{dn}=0$$
이 방정식을 사용하기 위해서는 유선의 각 위치에서의 곡률 반지름에 대한 정보가 주어야 한다.
'Physics > 유체역학' 카테고리의 다른 글
| 물이 일정하게 흘러나오는 구간은? (2) | 2024.01.13 |
|---|---|
| 더 빨리 비워지는 용기는? (0) | 2024.01.13 |
| 유체기둥이 더 높은 쪽은 (47) | 2023.12.02 |
| 양팔 저울은 어느 쪽으로 기울까? (29) | 2023.11.18 |
| 얼음이 녹으면 양팔 저울은 어느 쪽으로 기울까? (30) | 2023.11.17 |



