물체가 가장 아래에 내려왔을 때 장력은?

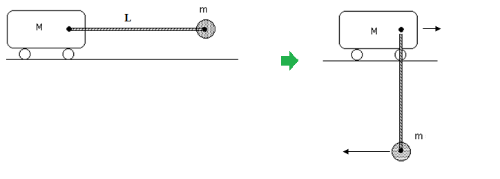
카트에 가벼운 막대로 연결된 물체가 그림과 같이 수평으로 있다가 운동을 시작한다. 물체가 가장 아래에 내려왔을 때 막대에 걸리는 장력은? 마찰은 무시한다.

풀이:

1. 수평방향의 외력이 없고, 처음 정지상태였으므로 질량중심의 수평 위치는 고정된다. 오른쪽 그림처럼 물체가 가장 아래에 내려왔을 때 속도를 $v$(수평 왼쪽)라면 카트의 속도는 $V=\frac{m}{M}v$(수평 오른쪽)이다. 

2. 역학적 에너지 보존을 이용하면 

$$mgL=\frac{1}{2}M{V}^2+\frac{1}{2}m{v}^2\to v^2=\frac{M}{m+M}2gL$$

3. 오른쪽 그림과 같은 상황에서 카트의 가속도는 $a_{\text{cart}}=0$이므로 이 순간 카트와 같은 속도로 움직이는 관성계에서 보면 물체는 $v+V=\frac{m+M}{M}v$의 속도를 가지고 수직원운동을 한다. 이 때 장력과 중력이 구심력 역할을 하므로

$$T-mg=m\frac{(v+V{)}^2}{L}=\frac{m}{L}{\left(\frac{m+M}{M}\right)}^2\frac{M}{m+M}2gL=2mg\frac{m+M}{M}$$

이므로 

$$T=mg(3+2\frac{m}{M})$$

4. 카트와 물체의 질량이 같은 경우: $T=5mg$, 카트가 매우 무거워서 고정이 되는 경우는 $T=3mg$이다. $M\ll m$이면 $M$이 매우 빠르게 움직이므로 $M$이 볼 때 $m$도 매우 빠르게 원운동을 하므로 구심력이 매우 커져야 하고, 따라서 장력도 매우 커져야 한다.

풀이2:

1. 막대가 수평에 대해 $\theta$만큼 기울어진 상태일 때 장력을 구해보자. 이 때 카트의 가속도는 $a_c=T\cos \theta /M$. 카트가 움직이는 수평속도를  ${\overrightarrow{v}}_M=\overrightarrow{u}$라면, 카트에서 볼 때 물체는 원운동을 하므로 물체의 속도를 ${\overrightarrow{v}}_m=\overrightarrow{u}+\overrightarrow{v}$로 쓰자. 여기서 $\overrightarrow{v}$는 막대에 수직한 방향이다. 카트와 같이 움직이는 계는 비관성계이므로 물체는 관성력 $m{a}_c=mT\cos \theta /M$(왼쪽)을 추가로 받고, 이 계에서 볼 때 물체는 $v$의 속력으로 원운동을 한다. 원운동에 필요한 구심력에는 장력, 관성력의 막대방향 성분, 중력의 막대방향 성분이 기여한다.

$$F_{\text{centripetal}}=T+\frac{m}{M}T\cos \theta \cos \theta -mg\sin \theta =m\frac{v^2}{L}$$

$$\to T=\frac{mg\sin \theta }{1+(m/M){\cos }^2\theta }(1+\frac{v^2}{gL\sin \theta })$$ 

2. 카트와 물체의 운동에너지는 상대 운동에너지와 질량중심 운동에너지의 합이다. 수평방향 외력이 없으므로 질량중심의 속도는 수직 성분 밖에 없고 크기는 $v_{cm}=\frac{m}{m+M}v\cos \theta$이다(질량중심의 수평성분은 상쇄되어야 한다). 그리고 카트와 물체 모두 수평방향으로 $u$의 속도성분이 있으므로 상대속도의 크기는 $v_{\text{rel}}=|{\overrightarrow{v}}_m-{\overrightarrow{v}}_M|=v$임을 알 수 있다. 따라서 

$$\frac{1}{2}\mu v_{\text{rel}}^2+\frac{1}{2}(m+M)v_{\text{cm}}^2=mgL\sin \theta$$ 여기서 $\mu =\frac{mM}{m+M}$는 환산질량이다.

$$\to v^2=\frac{m+M}{M}\frac{2gL\sin \theta }{1+(m/M){\cos }^2\theta }$$

이므로 

$$T=\frac{mg\sin \theta }{1+(m/M){\cos }^2\theta }(1+\frac{m+M}{M}\frac{2}{1+(m/M){\cos }^2\theta })$$