영상처리에서 한 픽셀의 수정을 위해서 주변 픽셀의 정보를 요구하는 윈도 기반 필터들은 일반적 연산 비용이 큰 편이다. 한 변의 길이가 $W$인 윈도를 사용할 때 $W^2$ 횟수의 픽셀을 참조해야 하므로 윈도가 클수록 그 비용은 제곱으로 증가한다. 선형 필터 중에는 $x$-방향과 $y$-방향 연산으로 각각 분리가 가능한 경우는 연산 비용이 필터의 크기에만 비례하도록 만들 수 있다. median 필터는 이런 분리가 안 되는 비선형 필터 중 하나다. 근사적으로 $x$-방향으로 median filtering을 하고, 그 결과를 $y$-방향으로 다시 median filtering을 하는 방법으로 연산을 줄이는 방법을 사용하기도 한다.
윈도가 움직이면서 윈도 내 모든 픽셀이 다 바뀌는 것이 아니라 움직이는 방향에 수직인 가장자리 픽셀만 바뀐다는 사실을 이용하면 각 픽셀의 윈도에서 median을 찾는 작업을 할 필요가 없다. 예를 들면 scanline 방향($x$-방향)으로 윈도를 움직이면서 median filter를 작용할 때, 윈도가 오른쪽으로 1 픽셀 움직이면 윈도의 왼쪽 가장자리의 수직 픽셀들은 새 윈도에서 사라지고, 기존 윈도의 오른쪽 수직 가장자리 앞의 픽셀들이 새로 들어온다. 따라서 각 스캔라인에서 처음 한 번만 윈도의 median을 찾으면 이후에는 윈도가 이동할 때 윈도를 나가는 픽셀과 새로 들어오는 픽셀 ($2W$) 개에 대해서 이전 median과 비교만 하면 된다. 이 방법은 비교 횟수가 윈도 크기에 1차적으로 비례하므로 연산 부담을 많이 줄일 수 있다. 이 방법은 사각형 모양의 윈도를 가지는 다른 필터(mean filter, max-filter, min-filter,...)에 대해서도 쉽게 적용할 수 있다.
// boundary region도 처리할 수 있게 수정함; 2021-04-18;
// window size = wx * wy;
// median = argmin(hist[i] >= halfArea)
int RunningMedianFilter(BYTE* image, int w, int h, int wx, int wy, BYTE* out) {
int hist[256], x;
int wxhalf = wx >> 1;
int wyhalf = wy >> 1;
wx = (wxhalf << 1) + 1; // size of window = odd number;
wy = (wyhalf << 1) + 1;
for (int y = 0, yw = 0; y < h; ++y, yw += w) {
// calc available area;
int wystart = max(0, y - wyhalf);
int wystop = min(h, y + wyhalf);
int wysize = wystop - wystart + 1;
int wxstart = 0;
int wxstop = wxhalf;
int halfArea = (wxstop * wysize + 1) >> 1;
// to avoid *w multiplication in y-step;
wystart *= w;
wystop *= w;
// initial histogram of topleft window;
memset(hist, 0, 256 * sizeof(int));
for (int iy = wystart; iy <= wystop; iy += w)
for (int ix = wxstart; ix <= wxstop; ++ix) hist[image[iy + ix]]++;
// find initial median;
int ltmed = hist[0]; // less_than_median;
int med = 0;
while (ltmed < halfArea) ltmed += hist[++med];
out[yw + 0] = med;
// left edge rgn;
for (x = 1; wxstop < wx; ++x) {
++wxstop;
halfArea = (wxstop * wysize + 1) >> 1;
for (int iy = wystart; iy <= wystop; iy += w) {
int v = image[iy + wxstop]; // (x=wxstop) strip enters;
++hist[v];
if (v <= med) ++ltmed;
}
while (ltmed >= halfArea) ltmed -= hist[med--];
while (ltmed < halfArea) ltmed += hist[++med];
out[yw + x] = med;
}
// central rgn;
for ( ; wxstop < w; ++x) {
++wxstop;
for (int iy = wystart; iy <= wystop; iy += w) {
int v = image[iy + wxstart]; // (x=wxstart) strip leaves;
--hist[v];
if (v <= med) --ltmed;
v = image[iy + wxstop]; // (x=wxstop) strip enters;
++hist[v];
if (v <= med) ++ltmed;
}
++wxstart;
while (ltmed >= halfArea) ltmed -= hist[med--];
while (ltmed < halfArea) ltmed += hist[++med];
out[yw + x] = med;
}
// right edge rgn;
for ( ; x <= w; ++x) {
for (int iy = wystart; iy <= wystop; iy += w) {
int v = image[iy + wxstart]; // (x=wxstart) strip leaves;
--hist[v];
if (v <= med) --ltmed;
}
++wxstart;
halfArea = ((wxstop - wxstart + 1) * wysize + 1) >> 1;
while (ltmed >= halfArea) ltmed -= hist[med--];
while (ltmed < halfArea) ltmed += hist[++med];
out[yw + x] = med;
}
}
return 1;
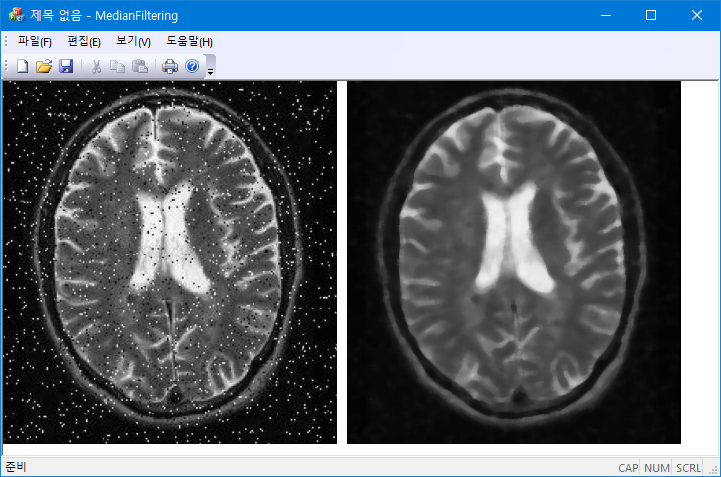
};wx=wy=7;
'Image Recognition > Fundamental' 카테고리의 다른 글
| Bicubic Interpolation (1) | 2010.01.14 |
|---|---|
| Bezier Curve을 이용한 Histogram Smoothing (0) | 2010.01.10 |
| Fant's Resampling (0) | 2008.12.17 |
| Bright Preserving Histogram Equalization with Maximum Entropy (0) | 2008.07.31 |
| Adaptive Binarization (2) | 2008.07.14 |











