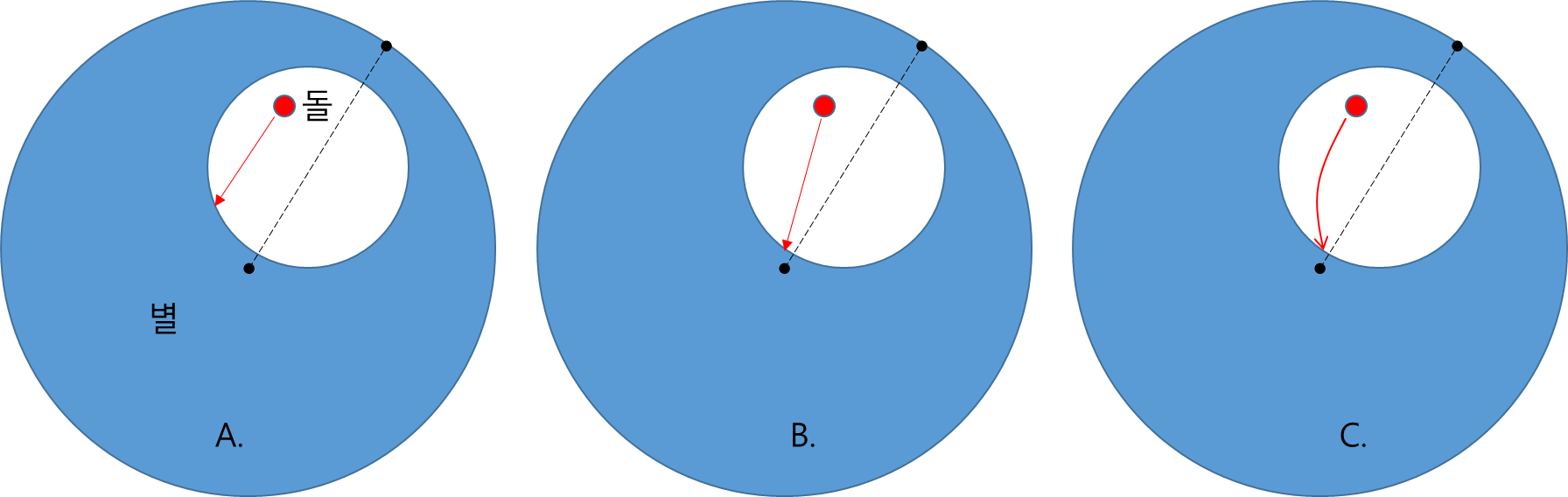
별 내부에 커다란 구형의 동굴이 있다. 이 동굴 내부에 돌을 가만히 놓았을 때 움직이는 경로로 맞는 것은?
'Physics > 역학' 카테고리의 다른 글
| 더 멀리 날아갈까? (0) | 2022.01.12 |
|---|---|
| 먼저 바닥에 닿는 다트는? (0) | 2022.01.12 |
| 회전하는 막대 중간 부분에서 인장력은 (0) | 2022.01.11 |
| 동전은 언제 책상 모서리에서 떨어지는가? (0) | 2022.01.10 |
| 고임목의 최소 높이는? (0) | 2022.01.08 |
별 내부에 커다란 구형의 동굴이 있다. 이 동굴 내부에 돌을 가만히 놓았을 때 움직이는 경로로 맞는 것은?

| 더 멀리 날아갈까? (0) | 2022.01.12 |
|---|---|
| 먼저 바닥에 닿는 다트는? (0) | 2022.01.12 |
| 회전하는 막대 중간 부분에서 인장력은 (0) | 2022.01.11 |
| 동전은 언제 책상 모서리에서 떨어지는가? (0) | 2022.01.10 |
| 고임목의 최소 높이는? (0) | 2022.01.08 |
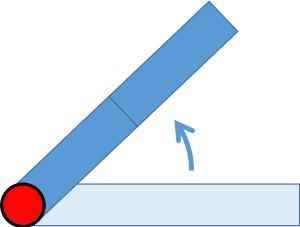
막대가 고정축에 대해 일정한 비율로 회전하고 있다. 막대 절반을 기준으로 안쪽 부분이 바깥쪽 부분을 당기는 힘(인장력: tensile stress)은 축에 걸리는 힘의 몇 배일까?
1. 1
2. 1/4
3. 1/2
4. 3/4
| 먼저 바닥에 닿는 다트는? (0) | 2022.01.12 |
|---|---|
| 돌이 움직이는 경로는? (0) | 2022.01.11 |
| 동전은 언제 책상 모서리에서 떨어지는가? (0) | 2022.01.10 |
| 고임목의 최소 높이는? (0) | 2022.01.08 |
| 지탱할 때 힘이 가장 많이 드는 지점는? (2) | 2022.01.07 |
책상 위를 구르는 동전이 책상 가장자리에 도달하면 모서리를 축으로 회전을 한다. (물론 모서리에서 마찰이 충분히 제공된다는 전제 하에서). 그러다가 모서리에서 떨어지게 되는데 언제일까?
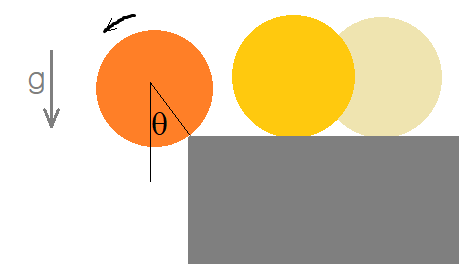
모서리를 축으로 $\theta$만큼 회전한 상황에서 에너지 보존을 쓰면 위치에 따른 속력을 구할 수 있다:
$$mgR= \tfrac{1}{2}mv^2 + \tfrac{1}{2} I_\text{coin} \omega^2 + mgR \cos \theta, \quad (v=R\omega, ~I_\text{coin} = \tfrac{1}{2} mR^2 )$$
$$ \rightarrow ~v^2 = \tfrac{4}{3} gR(1-\cos \theta)$$
동전의 질량중심은 모서리를 축으로 회전을 하는데 수직항력과 중력의 일부가 구심력을 만든다.
$$\sum F_c= - N+mg\cos \theta =\frac{mv^2}{R}$$
모서리와 접촉을 유지하기 위해서는 수직항력이 사라지지 않아야 하므로
$$N= mg \cos \theta -\frac{mv^2}{R} > 0 \quad \rightarrow \quad {v^2} < gR \cos \theta.$$
에너지 보존에서 얻은 결과와 결합하면 모서리에 접촉하고 있는 각 범위를 구할 수 있다.
$$ \tfrac{4}{3} (1-\cos \theta) < \cos \theta \quad \quad \therefore \theta <\cos^{-1}\left( \tfrac{4}{7}\right).$$
대략 $\theta = 55.15^\circ$에서 책상 모서리와 이별한다.
| 돌이 움직이는 경로는? (0) | 2022.01.11 |
|---|---|
| 회전하는 막대 중간 부분에서 인장력은 (0) | 2022.01.11 |
| 고임목의 최소 높이는? (0) | 2022.01.08 |
| 지탱할 때 힘이 가장 많이 드는 지점는? (2) | 2022.01.07 |
| 구르는 타이어 가장자리의 가속도는? (0) | 2022.01.06 |